Пусть граф g с n вершинами является деревом тогда выберите для g верные утверждения

Обновлено: 18.09.2024

Дерево: — Связный граф без какой-либо схемы называется деревом. Другими словами, дерево — это неориентированный граф G, который удовлетворяет любому из следующих эквивалентных условий:

Любые две вершины в G могут быть связаны единственным простым путем.
G ацикличен, и простой цикл образуется, если к G. добавлено любое ребро
G связан и не имеет циклов.
G подключен, но будет отключен, если какой-либо один край будет удален из G.
G связна и 3-вершинный полный граф K3 не является минором в G.

Например :

Некоторые теоремы, связанные с деревьями:

Доказательство: поскольку дерево (T) является связным графом, существует хотя бы один путь между каждой парой вершин в дереве (T). Теперь предположим, что между двумя вершинами a и b дерева (T) существуют два пути. Объединение этих двух путей будет содержать схему, и дерево (T) не может быть деревом. Следовательно, приведенное выше утверждение доказано.

Рисунок 3: Дерево (T)

Доказательство: между каждой парой вершин существует путь, поэтому мы предполагаем, что граф G связен. Схема в графе подразумевает, что существует по крайней мере одна пара вершин a и b, так что между a и b есть два различных пути. Поскольку G имеет один и только один путь между каждой парой вершин. У G не может быть никакой схемы. Следовательно, граф G является деревом.

Рисунок 4: данный граф G

Доказательство: пусть n будет количеством вершин в дереве (T).
Если n = 1, то число ребер = 0.
Если n = 2, то число ребер = 1.
Если n = 3, то число ребер = 2.

Следовательно, утверждение (или результат) верно для n = 1, 2, 3.

Пусть утверждение верно для n = m. Теперь мы хотим доказать, что это верно для n = m + 1.

Позволять быть ребром, соединяющим вершины, скажем, Vi и Vj. Поскольку G дерево, то существует только один путь между вершинами Vi и Vj. Следовательно, если мы удалим ребро e, это будет разъединенный граф на две составляющие, скажем, G1 и G2. Эти компоненты имеют менее чем m + 1 вершин, и схемы не существует, и, следовательно, каждый компонент G1 и G2 имеет вершины m1 и m2.

Следовательно, для n = m + 1 вершин имеется m ребер в дереве (T). По математической индукции граф точно имеет n-1 ребер.

Рисунок 5: Дано дерево T

Доказательство. Мы знаем, что минимальное количество ребер, необходимое для построения графа из n связанных вершин, равно (n-1) ребрам. Мы можем наблюдать, что удаление одного ребра из графа G сделает его разъединенным. Таким образом, связный граф из n вершин и (n-1) ребер не может иметь схему. Следовательно, граф G является деревом.

Рисунок 6: График G

Доказательство. Пусть граф G несвязен, тогда существуют хотя бы две компоненты, скажем, G1 и G2. Каждый компонент не имеет схемы, так как G является схемой. Теперь, чтобы связать граф G, нам нужно добавить одно ребро e между вершинами Vi и Vj, где Vi — вершина G1, а Vj — вершина компонента G2.
Теперь количество ребер в G = (n — 1) +1 = n.

Рисунок 7: Отключенный график

Теперь G является связным графом и без схемы с n вершинами и n ребрами, что невозможно, потому что связанный безконтурный граф является деревом, а дерево с n вершинами имеет (n-1) ребер. Таким образом, граф G с n вершинами, (n-1) ребрами и без схемы связен. Следовательно, данное утверждение доказано.

Рисунок 8: Связный граф G

Доказательство. Пусть граф G минимально связен, т.е. удаление одного края делает его отключенным. Поэтому схемы нет. Следовательно, граф G является деревом.
Наоборот, пусть граф G является деревом т.е. между каждой парой вершин существует один и только один путь, и мы знаем, что удаление одного ребра из пути делает граф отключенным. Следовательно, граф G минимально связен.

Рисунок 9: Минимально связанный график

Доказательство. Пусть число вершин в данном дереве T равно n и n> = 2. Поэтому число ребер в дереве T = n-1 с использованием приведенных выше теорем.

Сумма степеней должна быть разделена между n вершинами. Поскольку дерево T является связным графом, оно не может иметь вершину нулевой степени. Каждая вершина вносит как минимум одну сумму в вышеуказанную сумму. Таким образом, должно быть по крайней мере две вершины степени 1. Следовательно, каждое дерево с по крайней мере двумя вершинами имеет по крайней мере две подвесные вершины.

Рисунок 10: Здесь a, b и d являются вершинами данного графа

Доказательство: мы будем использовать одно наблюдение, что максимальное расстояние max d (v, w) от данной вершины v до любой другой вершины w происходит только тогда, когда w является висячей вершиной.

Теперь пусть T — дерево с n вершинами (n> = 2)

T должно иметь как минимум две подвесные вершины. Удалите все висячие вершины из T, тогда результирующий граф T 'останется деревом. Снова удалите подвесные вершины из T ', чтобы полученное T ”все еще было деревом с теми же центрами.

Обратите внимание, что все вершины, которые T имеет в качестве центров, все равно останутся центрами в T '-> T ”-> T”' ->….

продолжайте этот процесс, пока у оставшегося дерева не будет ни одной вершины, ни одного ребра. Таким образом, в конце концов, если есть одна вершина, это означает, что дерево T имеет один центр. Если есть одно ребро, то дерево T имеет два центра.

Доказательство: данная теорема доказана с помощью математической индукции. На уровне 0 (L = 0) есть только одна вершина на уровне (L = 1), есть только Вершины.

Теперь мы предполагаем, что утверждение верно для уровня (L-1).

Следовательно, максимальное количество вершин на уровне (L-1) , Поскольку мы знаем, что каждая вершина в двоичном дереве имеет максимум 2 вершины на следующем уровне, поэтому число вершин на уровне L в два раза больше, чем на уровне L-1.

Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного использования. Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.

Список вопросов теста

Вопрос 1

Что такое дерево?

Связный граф, не содержащий циклов
Неориентированный граф без петель и кратных ребер
Ориентированный граф без циклов
Граф, у которого могут быть ориентированные и неориентированные ребра

Вопрос 2

Узел дерева, который не имеет предков, называется…

сыном
листом
корнем
промежуточным узлом

Вопрос 3

Как называются предки узла, имеющие уровень на единицу меньше уровня этого узла?

детьми
родителями
братьями
сестрами

Вопрос 4

Укажите, сколько вершин — непосредственных потомков может иметь вершина произвольного дерева?

Любое количество
Две
Не более двух
Не менее одной

Вопрос 5

Узел, не имеющий потомков?

Корень
Лист
Предок
Родитель

Вопрос 6

Как называется дерево, в котором каждый узел может иметь не более двух сыновей?

Ориентированное
Бинарное
Неориентированное
Корневое

Вопрос 7

Сколько ребер в дереве с пятью вершинами?

Вопрос 8

Высотой дерева называется…

максимальное количество листьев
максимальное количество связей
максимальная длина пути от корня до листа
максимальное количество узл

Вопрос 9

Глубиной вершины называется…

длина пути в этой вершины в корень
максимальная длина пути от корня до листа
максимальное количество узлов
длина пути в эту вершину из корня

Вопрос 10

Пусть граф G с n вершинами является деревом.

Выберите для G НЕверное утверждение

5 г) λ(а) λ(в) λ(а В) Определить название столбца в таблице λ(а) λ(в) а) λ(а В) б) λ(а В) в) λ(а В) г) λ(а В) 17. Формула высказываний -это а) выражение, составленное из высказывательных переменных с помощью операций над высказываниями и обращающееся в конкретное высказывание при подстановке вместо этих переменных конкретных высказываний б) выражение, составленное из высказывательных переменных, обращающееся в конкретное высказывание при подстановке вместо этих переменных конкретных высказываний в) выражение, обращающееся в конкретное высказывание при подстановке вместо переменных конкретных высказываний г) выражение, составленное из высказывательных переменных 18. Выбрать верный порядок выполнения операций а) отрицание, импликация, конъюнкция, дизъюнкция, эквиваленция б) отрицание, конъюнкция, эквиваленция, дизъюнкция, импликация в) отрицание, эквиваленция, конъюнкция, дизъюнкция, импликация г) отрицание, конъюнкция, дизъюнкция, эквиваленция, импликация 19. Формула называется тавтологией, если для всех наборов значений переменных а) формула принимает одно и тоже значение, равное 0 б) формула верна в) формула принимает одно и тоже значение истинности, равное 1 г) формула принимает значение истинности, равное 1или Если для всех наборов значений переменных формула принимает одно и тоже значение истинности, равное 0, то ее называют а) тождественно- ложной б) тождественно-истинной в) тавтологией г) подформулой 5

6 Вариант 2 Выберите один правильный вариант ответа. Возможен только один вариант правильного ответа. 1. Дано универсальное множество U= и в нем подмножества A=, B=, C=.Найти а) U б) в) Оба ответа верны 4. Дано универсальное множество U= и в нем подмножества A=, B=, C=.Найти а) б) в) г) г) < (1,3), (1,5), (3,5), (1,6), (3,6)>8. Дано универсальное множество U= и в нем подмножества A=, B=, C=.Найти декартово (прямое) произведение, где а) б) в) U - г) 10. Выберите условия, каждое из которых является необходимым для того, чтобы связный граф с n вершинами был планарным ( m число ребер): а) б) m = 8 при n = 6 в) m 8 в) граф планарный 15. Пусть граф G с n вершинами является двудольным. Тогда: (Выберите для G верные утверждения.) а) в нем нет циклов четной длины б) граф связный в) степень каждой вершины не превосходит n - 2 г) граф содержит цикл, если каждая доля содержит не менее двух вершин 16. Для функции f, заданной вектором, определить, является ли она: в) самодвойственной 17. Для функции f, заданной вектором, определить, является ли она: в) Самодвойственной 18. Для функции f, заданной вектором, определить, является ли она: а) нелинейной в) Самодвойственной 19. Для функции определить, является ли она: в) Оба правильного ответа 20. Для функции определить, является ли она: б) немонотонной в) самодвойственной 8

11 18. Для функции f, заданной вектором, определить, является ли она: а) нелинейной в) Самодвойственной 55. Тип - дистрибутивный вопрос. 19. Для функции определить, является ли она: в) Оба правильного ответа 20. Для функции определить, является ли она: б) немонотонной в) самодвойственной 11

12 Вариант 4 Выберите один правильный вариант ответа. Возможен только один вариант правильного ответа. 1. Дано универсальное множество U= и в нем подмножества A=, B=, C=.Найти а) U б) в) Оба ответа верны 4. Дано универсальное множество U= и в нем подмножества A=, B=, C=.Найти а) б) в) г) г) < (1,3), (1,5), (3,5), (1,6), (3,6)>8. Дано универсальное множество U= и в нем подмножества A=, B=, C=.Найти декартово (прямое) произведение, где а) б) в) U - г) 10. Выберите условия, каждое из которых является необходимым для того, чтобы связный граф с n вершинами был планарным ( m число ребер): а) б) m = 8 при n = 6 в) m 14 в) граф планарный 15. Пусть граф G с n вершинами является двудольным. Тогда: (Выберите для G верные утверждения.) а) в нем нет циклов четной длины б) граф связный в) степень каждой вершины не превосходит n - 2 г) граф содержит цикл, если каждая доля содержит не менее двух вершин 16. Для функции f, заданной вектором, определить, является ли она: в) самодвойственной 17. Для функции f, заданной вектором, определить, является ли она: в) Самодвойственной 18. Для функции f, заданной вектором, определить, является ли она: а) нелинейной в) Самодвойственной 19. Для функции определить, является ли она: в) Оба правильного ответа 20. Для функции определить, является ли она: б) немонотонной в) самодвойственной 14

17 18. Для функции f, заданной вектором, определить, является ли она: а) нелинейной в) Самодвойственной 19. Для функции определить, является ли она: в) Оба правильного ответа 20. Для функции определить, является ли она: б) немонотонной в) самодвойственной 17

18 Ключи к тестам Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5 1 А Б А Б А 2 А Б А Б А 3 А А А А А 4 А Б А Б А 5 А В А В А 6 А А А А А 7 А Б А Б А 8 А Б А Б А 9 А Б А Б А 10 А В А В А 11 А Б Б Б Б 12 А А А А А 13 А А А А А 14 А А А А А 15 А А А А А 16 В Б Б Б Б 17 В А А А А 18 В А А А А 19 В А А А А 20 В Б Б Б Б 18

Деревья — это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.

Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.

дерево

Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.

Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .

Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.

Пример 1

График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.

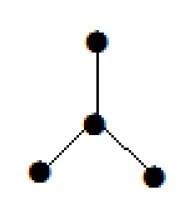
Примечание. Каждое дерево имеет как минимум две вершины первой степени.

Пример 2

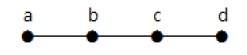
Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.

пример

Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.

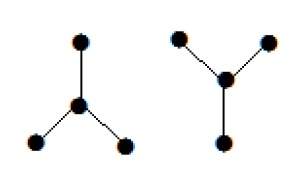
Охватывающие деревья

Пусть G — связный граф, тогда подграф H в G называется остовным деревом в G, если —

H это дерево
H содержит все вершины G.

Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.

Читайте также: