Коэффициент корреляции с урожайностью
Обновлено: 05.10.2024
3.5. Корреляционно-регрессионный анализ для определения степени влияния метеоусловий на урожайность.
При анализе урожайности, являющейся функцией очень многих факторов, часто возникает потребность количественно определить роль, степень влияния различных факторов. Одним из статистических методов, соответствующих поставленной задаче, является метод корреляционного анализа.
Для нахождения параметров а0 и а1 при линейной зависимости воспользуемся формулами из пункта 3.4.
Для нашего примера:
а1 = (6*43064 – 3488*74,5)/(6*2072762 – 3488 2 ) = 0,005
а0 = 12,4 + 0,005*581,3 = 15,3.
Отсюда уравнение регрессии будет иметь вид:
т.е. при изменении количества осадков на единицу, показатель урожайности изменится на 0,005.
Найдем коэффициент корреляции (r), который рассчитывается по формуле:
ai – коэффициент регрессии в уравнении связи,
x – среднее квадратическое отклонение факторного признака,
y – среднее квадратическое отклонение результативного признака.
Значения x и y рассчитаем по формулам, приведенным в предыдущем пункте, для чего воспользуемся суммами, рассчитанными для исчисления параметров связи. Перепишем эти суммы:
х=3488; у=74,5; х 2 =2072762; у 2 =932,13; n=6.
r = 0,005*(87/1,28)= 0,34,
т.е. теснота связи между количеством выпавших осадков и изменением урожайности небольшая. Что подтверждает расчеты, сделанные ранее в пункте 3.3.
Расчетная таблица за 6 лет.
3.6. Исчисление показателей колеблемости (устойчивости) урожайности во времени.
Ценные выводы об имеющихся резервах дальнейшего повышения урожайности дает сравнение урожайности хозяйств во времени, т.е. исчисление показателей колеблемости (устойчивости) урожайности.
Для этого необходимо определить средние уровни и показатели общей вариации урожайности зерновых (необходимые суммы и суммы квадратов определим по исходным данным таблицы 10).
Выравненные уровни по прямой линии yt
Отклонение от выравненного уровня y - yt
Средняя урожайность, ц с 1 га Y=Y/n
Дисперсия урожайности 2 = ( 2 / n) - 2 / n 2
Среднее квадратическое отклонение урожайности, ц с 1 га
Коэффициент вариации урожайности, % V0=(*100)/yср
По вышеприведенным формулам производим расчет показателей:
Средняя урожайность, ц с 1 га Yср=11,8
Дисперсия урожайности 2 =(2523,99/17) – (40200,25/289)=148,5 – 139=9,5
Среднее квадратическое отклонение урожайности, ц с 1 га =3,1
Коэффициент вариации урожайности, % V0=(3,1*100)/11,8=26,3.
Судя по коэффициентам вариации колеблемость урожайности зерновых в хозяйствах Тверской области довольно высока. Однако сделать вывод об устойчивости урожайности по этим данным нельзя, поскольку колеблемость определяется двумя группами причин: 1) тенденцией роста урожайности в динамике; 2) случайной колеблемостью урожайности около тенденции, определяющей саму урожайность.
Определим колеблемость урожайности зерновых по указанным двум источникам. Для этого проведем выравнивание урожайности по прямой линии и определим отклонения от выравненных уровней.
Динамика урожайности зерновых в Тверской области за 1985 – 2001 годы, ц с 1 га
Проведем выравнивание уровня урожайности зерновых в динамике по уравнению прямой линии Y=a+bt, где Y – урожайность, a – начальный сглаженный уровень, b – среднегодовой абсолютный прирост урожайности, t – номер года.
Для определения неизвестных параметров управления a и b составим систему из двух нормальных уравнений:
где n – число лет динамического ряда, равное 17 годам.
Необходимые для решения уравнения величины , t, yt и t 2 возьмем из таблицы 11. Подставим исходные данные в систему уравнений и решим ее:
Приведем к единице коэффициенты при а, разделив каждое уравнение соответственно на 17 и 153:
вычтем из второго уравнения первое и определим коэффициент b:
Рассчитаем коэффициент а, подставив значение b= - 0,5 в первое уравнение системы:
Следовательно, уравнение выравненного уровня урожайности в динамическом ряду составит Yt=16,3 – 1,5t, т.е. урожайность ежегодно уменьшается в среднем на 0,5 ц, начиная с уровня 16,3 ц, достигнутого к началу периода.
Исходя из полученных данных, продолжим анализ устойчивости урожайности во времени. Для этого вычислим следующие переменные:
Остаточная дисперсия урожайности 2 ост=((y - yt) 2 )/n
Остаточное среднее квадратическое отклонение, ц с 1 га
Остаточный коэффициент вариации, % Vост=ост*100/yср
Коэффициент устойчивости урожайности, % Ky=100 - Vост
Используя данные таблиц 10 и 11, находим вышеперечисленные показатели.
Остаточная дисперсия урожайности 2 ост=136,97/17=8,06
Остаточное среднее квадратическое отклонение, ц с 1 га ост=2,84
Остаточный коэффициент корреляции, % Vост=24,07
Коэффициент устойчивости урожайности, %
Как видно по уровню остаточного коэффициента вариации, случайная колеблемость, а следовательно, и неустойчивость урожайности зерновых довольно высока, что соответствует сделанному ранее выводу в пункте 3.1. В первую очередь, это связано с изменением метеорологических условий, которые оказывают большое влияние на урожайность зерновых.
Для наиболее точной характеристики устойчивости (колеблемости) урожайности найдем также факторную дисперсию, коэффициент случайной дисперсии, индекс корреляции по следующим формулам:
Факторная дисперсия 2 ф= 2 - 2 ост
Коэффициент случайной дисперсии К= 2 ост/ 2
Индекс корреляции R=1-К
Подставив значения, получим следующий результат:
Получив все необходимые данные, можно сделать вывод, что метеорологические условия оказывают наибольшее влияние на урожайность. Это показывает остаточная дисперсия (=8,06), которая характеризует вариацию урожайности, обусловленную причинами, не зависящими от человека, а также коэффициент случайной дисперсии (К=0,85), характеризующий степень зависимости урожайности от случайных факторов, т.е. независящих от человека причин.
Раздел: Статистика
Количество знаков с пробелами: 73603
Количество таблиц: 18
Количество изображений: 3
Проверка на существенность уравнения регрессии осуществляется с помощью F-критерия Фишера. Фактическое значение F-критерия определяется по формуле:

,
где S 2 воспр – дисперсия воспроизведенная факторами,

S 2 воспр=,
Wвоспр - объем вариации,

;
m-1 – число степеней свободы; m – число параметров уравнения, включающее а0;

S 2 ост – остаточная дисперсия, ;
Wост – объем остаточной вариации (сумма квадратов отклонений),

Wост=W0-Wвоспр, W0 – общий объем вариации, W0=Σ(у-) 2 .
Фактическое значение F-критерия сопоставляется с табличным (приложение 1), найденным при доверительном уровне вероятности суждения – 0,95 и числе степеней свободы двух сравниваемых дисперсий. Если расчетное значение F-критерия больше табличного, то уравнение признается значимым.
Для оценки значимости индекса корреляции F-критерий вычисляется по формуле:

,
где n – число наблюдений; m – число параметров уравнений (α0, α 1, α 2 и т.д.).
Расчетное значение F сравнивается с табличным для принятого уровня вероятности и числе степеней свободы: к1=m-1 и к2=n-m.
Эта тема планировалась более 10 лет назад и вот, наконец, я здесь…. И вы здесь! И это замечательно! Даже не то слово. Это корреляционно.
Материал данной темы состоит из двух уровней:
– начального, для всех – вплоть до студенток психологических и социологических факультетов, школьников, бабушек, дедушек, etc и
– продвинутого, где я разберу более редкие задачи, а некоторые даже не буду разбирать :)
В результате вы научитесь БЫСТРО решать типовые задачи (видео прилагается) и для самых ленивых есть калькуляторы. И пока не запамятовал, хочу порекомендовать корреляционно-регрессионный анализ для ваших научных работ и практических исследований – наряду со статистическими гипотезами, это самая настоящая находка в плане новизны и творческих изысканий.
Оглавление:
…и в этот момент я благоговейно улыбаюсь – как здорово, что все мы здесь сегодня собрались:

Имеются выборочные данные по студентам: – количество прогулов за некоторый период времени и – суммарная успеваемость за этот период:
И сразу обращаю внимание, что в условии приведены несгруппированные данные. Помимо этого варианта, есть задачи, где изначально дана комбинационная таблица, и их мы тоже разберём. Сначала одно, затем другое.
1) высказать предположение о наличии и направлении корреляционной зависимости признака-результата от признака-фактора и построить диаграмму рассеяния;
2) анализируя диаграмму рассеяния, сделать вывод о форме зависимости;
3) найти уравнение линейной регрессии на , выполнить чертёж;
4) вычислить линейный коэффициент корреляции, сделать вывод;
5) вычислить коэффициент детерминации, сделать вывод,
и позже будет ещё 5-6 пунктов для продвинутых читателей (см. конец урока).
Решение:
1) Прежде всего, повторим, что такое корреляционная зависимость. Очевидно, что чем больше студент прогуливает, тем более вероятно, что у него плохая успеваемость. Но всегда ли это так? Нет, не всегда. Успеваемость зависит от многих факторов. Один студент может посещать все пары, но все равно учиться посредственно, а другой – учиться неплохо даже при достаточно большом количестве прогулов. Однако общая тенденция состоит в том, что с увеличением количества прогулов средняя успеваемость студентов будет падать. Такая нежёсткая зависимость и называется корреляционной.
Проверить выдвинутое предположение проще всего графически, и в этом нам поможет:
диаграмма рассеяния
И здесь я анонсирую дальнейшие действия: сейчас нам предстоит найти уравнение прямой, ТАКОЙ, которая проходит максимально близко к эмпирическим точкам, а также оценить тесноту линейной корреляционной зависимости – насколько близко расположены эти точки к построенной прямой.
Технически существует два пути решения:
– сначала найти уравнение прямой и затем оценить тесноту зависимости;
– сначала найти тесноту и затем составить уравнение.
В практически задачах чаще встречается второй вариант, но я начну с первого, он более последователен. Построим:
3) уравнение линейной регрессии на
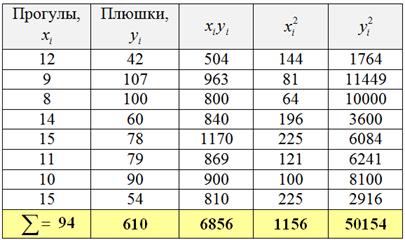
Это и есть та самая оптимальная прямая , которая проходит максимально близко к эмпирическим точкам. Обычно её находят методом наименьших квадратов, и мы пойдём знакомым путём. Заполним расчётную таблицу:
Обратите внимание, что в отличие от задач урока МНК у нас появился дополнительный столбец , он потребуется в дальнейшем, для расчёта коэффициента корреляции.
Коэффициенты функции найдём из решения системы:
Сократим оба уравнения на 2, всё попроще будет:
Систему решим по формулам Крамера:
, значит, система имеет единственное решение.
И проверка forever, подставим полученные значения в левую часть каждого уравнения исходной системы:
в результате получены соответствующие правые части, значит, система решена верно.
Таким образом, искомое уравнение регрессии:
Найдём пару удобных точек для построения прямой:
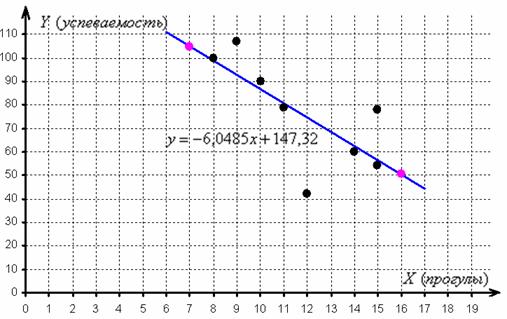
отметим их на чертеже (малиновый цвет) и проведём линию регрессии:
Говорят, что уравнение регрессии аппроксимирует (приближает) эмпирические данные (точки), и с помощью него можно интерполировать (оценить) неизвестные промежуточные значения, так при количестве прогулов среднеожидаемая успеваемость составит балла.
Второй вопрос касается тесноты зависимости. Очевидно, что чем ближе эмпирические точки к прямой, тем теснее линейная корреляционная зависимость – тем уравнение регрессии достовернее отражает ситуацию, и тем качественнее полученная модель. И наоборот, если многие точки разбросаны вдали от прямой, то признак зависит от вовсе не линейно (если вообще зависит) и линейная функция плохо отражает реальную картину.
Прояснить данный вопрос нам поможет:
4) линейный коэффициент корреляции
Этот коэффициент как раз и оценивает тесноту линейной корреляционной зависимости и более того, указывает её направление (прямая или обратная). Его полное название: выборочный линейный коэффициент пАрной корреляции Пирсона :)
И в зависимости от фантазии автора задачи вам может встретиться любая комбинация этих слов. Теперь нас не застанешь врасплох, Карл.
Линейный коэффициент корреляции вычислим по формуле:
, где: – среднее значение произведения признаков, – средние значения признаков и – стандартные отклонения признаков. Числитель формулы имеет особый смысл, о котором я расскажу, когда мы будем разбирать второй способ решения.
Осталось разгрести всё это добро :) Впрочем, все нужные суммы уже рассчитаны в таблице выше. Вычислим средние значения:
Стандартные отклонения найдём как корни из соответствующих дисперсий, вычисленных по формуле:
Таким образом, коэффициент корреляции:
И расшифровка: коэффициент корреляции может изменяться в пределах и чем он ближе по модулю к единице, тем теснее линейная корреляционная зависимость – тем ближе расположены точки к прямой, тем качественнее и достовернее линейная модель. Если либо , то речь идёт о строгой линейной зависимости, при которой все эмпирические точки окажутся на построенной прямой. Наоборот, чем ближе к нулю, тем точки рассеяны дальше, тем линейная зависимость выражена меньше. Однако в последнем случае зависимость всё равно может быть! – например, нелинейной или какой-нибудь более загадочной. Но до этого мы ещё дойдём. А у кого не хватит сил, донесём :)
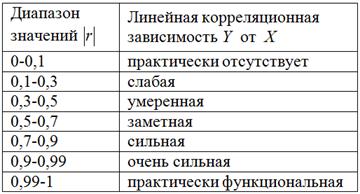
Для оценки тесноты связи будем использовать уже знакомую шкалу Чеддока:
При этом если , то корреляционная связь обратная, а если , то прямая.
В нашем случае , таким образом, существует сильная обратная линейная корреляционная зависимость – суммарной успеваемости от – количества прогулов.
Линейный коэффициент корреляции – это частный аналог эмпирического корреляционного отношения. Но в отличие от отношения, он показывает не только тесноту, но ещё и направление зависимости, ну и, конечно, здесь определена её форма (линейная).
5) Коэффициент детерминации
– это частный аналог эмпирического коэффициента детерминации – есть квадрат коэффициента корреляции:
– коэффициент детерминации показывает долю вариации признака-результата , которая обусловлена воздействием признака-фактора .
В нашей задаче:
– таким образом, в рамках построенной модели успеваемость на 51,74% зависит от количества прогулов. Оставшаяся часть вариации успеваемости (48,26%) обусловлена другими причинами.
Задание выполнено
Но точку ставить рано. Теперь второй способ решения, в котором мы сначала находим коэффициент корреляции, а затем уравнение регрессии.
Линейный коэффициент корреляции вычислим по формуле:
, где – стандартные отклонения признаков .
Член в числителе называют корреляционным моментом или коэффициентом ковариации (совместной вариации) признаков, он рассчитывается следующим образом: , где – объём статистической совокупности, а – средние значения признаков. Данный коэффициент показывает, насколько согласованно отклоняются пАрные значения от своих средних в ту или иную сторону. Формулу можно упростить, в результате чего получится ранее использованная версия, без подробных выкладок: . Но сейчас мы пойдём другим путём.
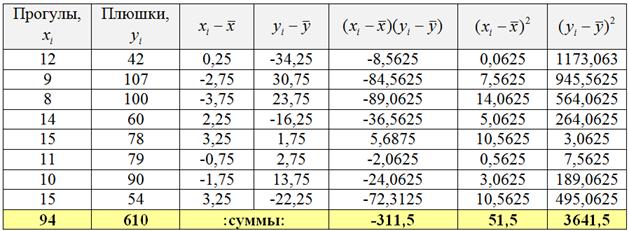
Заполним расчётную таблицу:
При этом сначала рассчитываем левые нижние суммы и средние значения признаков:
и только потом заполняем оставшиеся столбцы таблицы. О том, как быстро выполнить эти вычисления в Экселе, будет видео ниже!
Вычислим коэффициент ковариации:
.
Стандартные отклонения вычислим как квадратные корни из дисперсий:
Таким образом, коэффициент корреляции:
И если нам известны значения , то коэффициенты уравнения регрессии легко рассчитать по следующим формулам:
Таким образом, искомое уравнение:
Теперь смотрим ролик о том, как это всё быстро подсчитать и построить:

Как вычислить коэффициент корреляции и найти уравнение регрессии? (Ютуб)
Если под рукой нет Экселя, ничего страшного, разобранную задачу не так трудно решить в обычной клетчатой тетради. А если Эксель есть и времени нет, то можно воспользоваться моим калькулятором. Да, вы можете найти аналоги в Сети, но, скорее всего, это будет не совсем то, что нужно ;)
Какой способ решения выбрать? Ориентируйтесь на свой учебный план и методичку. По умолчанию лучше использовать 2-й способ, он несколько короче, и, вероятно, потому и встречается чаще. Кстати, если вам нужно построить ТОЛЬКО уравнение регрессии, то уместен 1-й способ, ибо там мы находим это уравнение в первую очередь.
Следующая задача много-много лет назад была предложена курсантам местной школы милиции (тогда ещё милиции), и это чуть ли не первая задача по теме, которая встретилась в моей профессиональной карьере. И я безмерно рад предложить её вам сейчас, разумеется, с дополнительными пунктами:)

В результате независимых опытов получены 7 пар чисел:
…да, числа могут быть и отрицательными.
По данным наблюдений вычислить линейный коэффициент корреляции и детерминации, сделать выводы. Найти параметры линейной регрессии на , пояснить их смысл. Изобразить диаграмму рассеяния и график регрессии. Вычислить , что означают полученные результаты?
Из условия следует, что признак , очевидно, зависит от (ибо кто ж делает бессвязные опыты). Однако помните, что корреляционная зависимость и причинно-следственная связь – это не одно и то же! (прочитайте, если до сих пор не прочитали!). Поэтому, если в задаче просто предложены два числовых ряда (без контекста), то можно говорить лишь о зависимости корреляционной, но не о причинно-следственной.
Все данные уже забиты в Эксель, и вам осталось аккуратно выполнить расчёты. В образце я решил задачу вторым, более распространённым способом. И, конечно же, выполните проверку первым путём.
Следует отметить, что в целях экономии места я специально подобрал задачи с малым объёмом выборки. На практике обычно предлагают 10 или 20 пар чисел, реже 30, и максимальная выборка, которая мне встречалась в студенческих работах – 100. …Соврал малость, 80.
И сейчас я вас приглашаю на следующий урок, назову его Уравнение линейной регрессии, где мы рассчитаем и найдём всё то же самое – только для комбинационной группировки. Плюс немного глубже копнём уравнения регрессии (их два).
Решения и ответы:
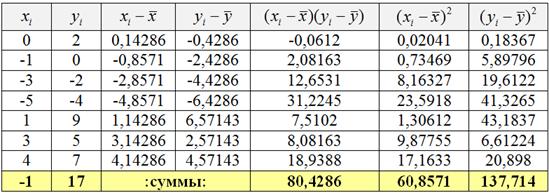
Пример 68. Решение: вычислим суммы и средние значения признаков , и заполним расчётную таблицу:
Вычислим коэффициент ковариации:
.
Вычислим средние квадратические отклонения:
Вычислим коэффициент корреляции:
, таким образом, существует сильная прямая корреляционная зависимость от.
Вычислим коэффициент детерминации:
– таким образом, 77,19% вариации признака обусловлено изменением признака . Остальная вариация (22,81%) обусловлена другими факторами.
Вычислим коэффициенты линейной регрессии :
Таким образом, искомое уравнение регрессии:
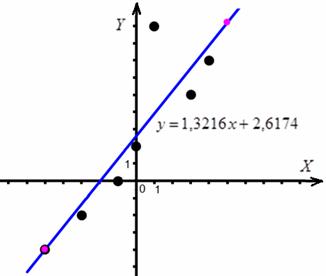
Найдём пару точек для построения прямой:
и выполним чертёж:
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

где x·y , x , y - средние значения выборок; σ(x), σ(y) - среднеквадратические отклонения.
Кроме того, коэффициент линейной парной корреляции Пирсона может быть определен через коэффициент регрессии b : , где σ(x)=S(x), σ(y)=S(y) - среднеквадратические отклонения, b - коэффициент перед x в уравнении регрессии y=a+bx .
Другие варианты формул:
или
Кxy - корреляционный момент (коэффициент ковариации)

Для нахождения линейного коэффициента корреляции Пирсона необходимо найти выборочные средние x и y , и их среднеквадратические отклонения σx = S(x), σy = S(y):
Линейный коэффициент корреляции указывает на наличие связи и принимает значения от –1 до +1 (см. шкалу Чеддока). Например, при анализе тесноты линейной корреляционной связи между двумя переменными получен коэффициент парной линейной корреляции, равный –1 . Это означает, что между переменными существует точная обратная линейная зависимость.
Вычислить значение коэффициента корреляции можно по заданным средним выборки, либо непосредственно по исходным табличным данным.
Геометрический смысл коэффициента корреляции: rxy показывает, насколько различается наклон двух линий регрессии: y(x) и х(у) , насколько сильно различаются результаты минимизации отклонений по x и по y . Чем больше угол между линиями, то тем больше rxy .
Знак коэффициента корреляции совпадает со знаком коэффициента регрессии и определяет наклон линии регрессии, т.е. общую направленность зависимости (возрастание или убывание). Абсолютная величина коэффициента корреляции определяется степенью близости точек к линии регрессии.
- |rxy| ≤ 1;, -1≤x≤1
- если X и Y независимы, то rxy=0 , обратное не всегда верно;
- если |rxy|=1 , то Y=aX+b , |rxy(X,aX+b)|=1 , где a и b постоянные, а ≠ 0;
- |rxy(X,Y)|=|rxy(a1X+b1, a2X+b2)|, где a1, a2, b1, b2 – постоянные.
Инструкция . Укажите количество исходных данных. Полученное решение сохраняется в файле Word (см. Пример нахождения уравнения регрессии). Также автоматически создается шаблон решения в Excel . Подробнее.

Типовые задания (см. также нелинейная регрессия)
Типовые задания
Исследуется зависимость производительности труда y от уровня механизации работ x (%) по данным 14 промышленных предприятий. Статистические данные приведены в таблице.
Требуется:
1) Найти оценки параметров линейной регрессии у на х. Построить диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.
2) На уровне значимости α=0.05 проверить гипотезу о согласии линейной регрессии с результатами наблюдений.
3) С надежностью γ=0.95 найти доверительные интервалы для параметров линейной регрессии.
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
- Рассчитать коэффициент линейной парной корреляции и построить уравнение линейной парной регрессии одного признака от другого. Один из признаков, соответствующих Вашему варианту, будет играть роль факторного (х), другой – результативного (y). Причинно-следственные связи между признаками установить самим на основе экономического анализа. Пояснить смысл параметров уравнения.
- Определить теоретический коэффициент детерминации и остаточную (необъясненную уравнением регрессии) дисперсию. Сделать вывод.
- Оценить статистическую значимость уравнения регрессии в целом на пятипроцентном уровне с помощью F-критерия Фишера. Сделать вывод.
- Выполнить прогноз ожидаемого значения признака-результата y при прогнозном значении признака-фактора х, составляющим 105% от среднего уровня х. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(1) = 4.01*1 + 99.18 = 103.19
y(2) = 4.01*2 + 99.18 = 107.2
. . .
Значимость коэффициента корреляции
Выдвигаем гипотезы:
H0: rxy = 0, нет линейной взаимосвязи между переменными;
H1: rxy ≠ 0, есть линейная взаимосвязь между переменными;
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезе H1 ≠ 0, надо вычислить наблюдаемое значение критерия (величина случайной ошибки):
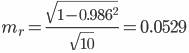
r - Δr ≤ r ≤ r + Δr
Δr = ±tтаблmr = ±2.228 • 0.0529 = 0.118
0.986 - 0.118 ≤ r ≤ 0.986 + 0.118
Доверительный интервал для коэффициента корреляции: 0.868 ≤ r ≤ 1
Анализ точности определения оценок коэффициентов регрессии
Статистическая значимость коэффициента регрессии подтверждается (62.62>2.228).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (tтабл=2.228):
(a - tтабл·Sa; a + tтабл·S a)
(3.6205;4.4005)
(b - tтабл·Sb; b + tтабл·Sb)
(96.3117;102.0519)
Fkp = 4.96. Поскольку F > Fkp, то коэффициент детерминации статистически значим (см. критерий Фишера).
Значимость линейного коэффициента корреляции Пирсона. tнабл = rxy· √ n-2 √ 1-rxy 2 = 0.2872· √ 9 √ 1-0.2872 2 = 0.9
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=n-m-1=11-1-1=9 находим tкрит: tкрит(n-m-1;α/2) = tкрит(9;0.025) = 2.262, где m=1 - количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции Пирсона признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл , то принимаем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - не значим
В парной линейной регрессии t 2 r = t 2 b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
Интервальная оценка для линейного коэффициента корреляции Пирсона ( rxy - tкрит· 1-rxy 2 √ n ; rxy + tкрит· 1-rxy 2 √ n )
Доверительный интервал для коэффициента корреляции ( 0.29 - 2.262· 1-0.29 2 √ 11 ; 0.29 + 2.262· 1-0.29 2 √ 11 ) Доверительный интервал для линейного коэффициента корреляции Пирсона: r(-0.9129;0.3386)
Читайте также:

