Среди семян ржи 0 4 семян сорняков какова вероятность что среди 500 сорняков

Обновлено: 30.06.2024

Вопрос по математике:

Среди семян ржи 0,4 % семян сорняков. Какова вероятность при случайном отборе 500 семян обнаружить 5 семян сорняков.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок - бесплатно!

24.07.2016 13:50
Математика
remove_red_eye 13079
thumb_up 12

Ответы и объяснения 1

Вероятность - это отношение того, что нужно к тому , что есть вообще!
следовательно нужно 5/500=0,01% вероятность того что из 500 можно обнаружить 5 семян сорняков

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи - смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Решение. Применение асимптотической формулы (38) для случая, когда вероятность р близка к нулю, приводит к значительному отклонению от точного значения .

Если вероятность появления события А в каждом из п независимых испытаний мала, а число испытаний п достаточно велико, то вероятность того, что событие А наступит т раз, вычисляется приближенно по формуле

Формулу (39) применяют в тех случаях, когда . При этом чем больше число п и меньше число р, тем точнее результат по этой формуле. По условию задачи . Тогда . Применяя (39), получим

Закон Пуассона , где λ равна среднему числу появления событий в одинаковых независимых испытаниях, т.е. λ = n × p, где p – вероятность события при одном испытании, e = 2,71828 .

В случае, когда n велико, а λ = p·n > 10 формула Пуассона дает очень грубое приближение и для расчета P_n(m) используют локальную и интегральную теоремы Муавра-Лапласа.

Числовые характеристики случайной величины Х

Дисперсия распределения Пуассона
D[X] = λ

Пример №1 . Семена содержат 0.1% сорняков. Какова вероятность при случайном отборе 2000 семян обнаружить 5 семян сорняков?
Решение.
Вероятность р мала, а число n велико. np = 2 5 e -5 /5! = 0.03609
Математическое ожидание: M[X] = λ = 2
Дисперсия: D[X] = λ = 2

Пример №2 . Среди семян ржи имеется 0.4% семян сорняков. Составить закон распределения числа сорняков при случайном отборе 5000 семян. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. Математическое ожидание: M[X] = λ = 0.004*5000 = 20. Дисперсия: D[X] = λ = 20
Закон распределения:

X	0	1	2	…	m	…
P	e -20	20e -20	200e -20	…	20 m e -20 /m!	…

Пример №3 . На телефонной станции неправильное соединение происходит с вероятностью 1/200. Найдите вероятность того, что среди 200 соединений произойдет:
а) ровно одно неправильное соединение;
б) меньше чем три неправильных соединения;
в) больше чем два неправильных соединения.
Решение. По условию задачи вероятность события мала, поэтому используем формулу Пуассона (15).
а) Задано: n = 200, p = 1/200, k = 1. Найдем P₂₀₀(1).
Получаем: . Тогда P₂₀₀(1) ≈ e -1 ≈ 0,3679.
б) Задано: n = 200, p = 1/200, k 2. Найдем P₂₀₀(k > 2).
Эту задачу можно решить проще: найти вероятность противоположного события, так как в этом случае нужно вычислить меньше слагаемых. Принимая во внимание предыдущий случай, имеем
P₂₀₀(k>2) = 1-P₂₀₀(k≤2) = 1-P₂₀₀(k n является достаточно большим, а p — достаточно малым; положим np = a , где a — некоторое число. В этом случае искомая вероятность определяется формулой Пуассона:

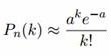
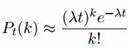
где λ — интенсивность потока событий, то есть среднее число событий, которые появляются в единицу времени.

Пример №4 . Вероятность того, что деталь бракованная, равна 0.005. проверяется 400 деталей. Укажите формулу вычисления вероятности того, что больше 3 деталей оказались с браком.

Пример №5 . Вероятность появления бракованных деталей при их массовом производстве равна p. определить вероятность того, что в партии из N деталей содержится а) ровно три детали; б) не более трех бракованных деталей.
p=0,001; N = 4500
Решение.
Вероятность р мала, а число n велико. np = 4.5 - λ = e -4.5 = 0.01111
P(1) = λe -λ = 4.5e -4.5 = 0.04999

Тогда вероятность того, что в партии из N деталей содержится ровно три детали, равна:

Тогда вероятность того, что в партии из N деталей содержится не более трех бракованных деталей:
P(x Пример №6 . Автоматическая телефонная станция получает в среднем за час N вызовов. Определить вероятность того, что за данную минуту она получит: а) ровно два вызова; б) более двух вызовов.
N = 18
Решение.
За одну минуту АТС в среднем получает λ = 18/60 мин. = 0,3
Считая, что случайное число X вызовов, поступивших на АТС за одну минуту,
подчиняется закону Пуассона, по формуле найдем искомую вероятность

Найдем ряд распределения X.
Здесь λ = 0.3
P(0) = e - λ = e -0.3 = 0.7408
P(1) = λe -λ = 0.3e -0.3 = 0.2222

Вероятность того, что за данную минуту она получит ровно два вызова:
P(2) = 0,03334
Вероятность того, что за данную минуту она получит более двух вызовов:
P(x>2) = 1 – 0,7408 – 0,2222 – 0,03334 = 0,00366

Пример №7 . Рассматриваются два элемента, работающих независимо друг от друга. Продолжительность времени безотказной работы имеет показательное распределение с параметром λ1 = 0,02 для первого элемента и λ2 = 0,05 для второго элемента. Найти вероятность того, что за 10 часов: а) оба элемента будут работать безотказно; б) только Вероятность того, что за 10 часов элемент №1 не выйдет из строя:
Рещение.
P₁(0) = e -λ1*t = e -0.02*10 = 0,8187

Вероятность того, что за 10 часов элемент №2 не выйдет из строя:
P₂(0) = e -λ2*t = e -0.05*10 = 0,6065

а) оба элемента будут работать безотказно;
P(2) = P₁(0)*P₂(0) = 0,8187*0,6065 = 0,4966
б) только один элемент выйдет из строя.
P(1) = P₁(0)*(1-P₂(0)) + (1-P₁(0))*P₂(0) = 0.8187*(1-0.6065) + (1-0.8187)*0.6065 = 0.4321

Пример №7 . Производство даёт 1% брака. Какова вероятность того, что из взятых на исследование 1100 изделий выбраковано будет не больше 17?
Примечание: поскольку здесь n*p =1100*0.01=11 > 10, то необходимо использовать теорему Лапласа.

Или так:
Число сыгранных матчей в первом круге:

И за 2 круга будет сыграно 105*2 = 210 (игр)

Раскроем скобки

(4x^2 - 24x) - (10x-4x^2)

4x^2 - 24x - 10x + 4x^2 =

Галя прочитала 25\% книги, а если она прочитает ещё 77 страниц, то будет прочитано 60\% все книги. Сколько всего страниц в книге

Из двух поселков Одновременно навстречу друг другу выехали два автомобиля один со скоростью 106 км ч и проехал до встречи пути д

1)Вычислите площадь круга, диаметр которого равен 1) 18 см; 2) 3,6 м. 2) Длина окружности равна 100,48 см. Найдите площадь круга

Задача 47. В отделении 10 стрелков, из них 3 отличных, 5 хороших и 2 посредственных. Известно, что вероятность попадания в цель отличным стрелком - 0,9, хорошим - 0,8, и стреляющим удовлетворительно - 0,6. Из строя наугад вызывается один стрелок для производства выстрела по цели. Какова вероятность попадания в цель этим стрелком?

Решение. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий H1, H2, …, Hn, образующих полную группу (гипотез), в соответствии с Формулой полной вероятности, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А, т. е. P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+…+P(Hn)P(A/Hn)= .

Пусть событие А – стрелок попал в цель. Гипотезы: H1 – стрелок отличный; H2 – стрелок хороший; H3 – стрелок посредственный. Вероятности этих гипотез следующие: ; ; .

Условные вероятности поражения цели по этим гипотезам даны:

P(A/H1)=0,9; P(A/H2)=0,8; P(A/H3)=0,6

Тогда, согласно формуле полной вероятности, искомая вероятность попадания в цель будет равна

P(A)=0,3×0,9+0,5×0,8+0,2×0,6=0,79.

Задача 48. В условиях предыдущей задачи 47 будем считать, что вызванный наугад стрелок произвел выстрел и попал в цель. Требуется определить вероятности, характеризующие его принадлежность к различным категориям стрелков.

Решение. В соответствии с Формулами Байеса, вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на условную вероятность события по этой гипотезе, деленному на полную вероятность события:

В нашей задаче событие А – стрелок попал в цель; гипотезы Н1 – стрелял отличный стрелок; Н2 – стрелял хороший стрелок; Н3 – стрелял посредственный стрелок.

Априорные[1] (доопытные) вероятности гипотез нам известны: Р(Н1)=0,3; Р(Н2)=0,5; Р(Н3)=0,2. Условные вероятности попадания в цель по этим гипотезам даны: Р(А/Н1)=0,9; Р(А/Н2)=0,8; Р(А/Н3)=0,6. Полная вероятность попадания в цель Р(А)=0,79.

Тогда апостериорные[2] (послеопытные) вероятности гипотез будут равны

Заметим, что сумма вероятностей гипотез после испытания всегда равна единице. Для нашего примера .

Задача 49. Всхожесть семян данного растения составляет 90 %. Найти вероятность того, что из пяти посеянных семян взойдут: а) четыре; б) не менее четырех.

Решение. Воспользуемся Формулой Бернулли. Если производится П независимых испытаний, при каждом из которых вероятность осуществления событий А постоянна и равна Р, а вероятность противоположного события равна Q=1-P, то вероятность Рп(т) того, что при этом событие А осуществляется ровно Т раз, вычисляется по формуле

Где есть число сочетаний из П элементов по Т.

А) По условию задачи вероятность всхожести семян Р=0,9; тогда Q=0,1; в данном случае П=5 и Т=4. Подставляя эти данные в формулу Бернулли (1), получим

Б) Искомое событие А состоит в том, что из пяти посеянных семян взойдут или четыре, или пять. Таким образом, Р(А)=Р5(4)+Р5(5). Первое слагаемое уже найдено. Для вычисления второго снова применяем формулу (1):

Следовательно, Р(А)=0,328+0,591=0,919.

Задача 50. Вероятность появления события А в каждом из 625 испытаний равна 0,64. Найти вероятность того, что событие А в этих испытаниях появиться ровно 415 раз.

Решение. Если число испытаний П велико, то применение формулы Бернулли приводит к громоздким вычислениям. Использование этой формулы становиться практически невозможным. В таких случаях применяют приближенную формулу, которая выражает суть локальной теоремы Лапласа.

Если вероятность наступления события А в каждом из П независимых испытаний постоянна и равна Р (Р отлично от нуля и единицы), а число П достаточно велико, то вероятность Рп(т) того, что в этих испытаниях событие А наступит Т раз (безразлично, в какой последовательности) вычисляется приближенно по формуле

Имеются готовые таблицы значений функции J(х) (см. табл. 1 Приложения).

По табл. 1 находим, что J(1,25)=0,1826. Подставив это значение в (2), получим

Задача 51. Среди семян ржи 0,04 % сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?

Решение. Применение асимптотической формулы (2) для случая, когда вероятность Р близка к нулю, приводит к значительному отклонению от точного значения Рп(т). При малых значениях Р (и при малых значениях Q) применяют асимптотическую формулу Пуассона.

Если вероятность появления события А в каждом из П независимых испытаний мала, а число испытаний П достаточно велико, то вероятность того, что событие А наступит Т раз, вычисляется приближенно по формуле

Где L=Пр.

Формулу (3) применяют в тех случаях, когда L£10. При этом чем больше число П И меньше число Р, тем точнее результат по этой формуле. По условию задачи П=5000, Т=5, Р=0,0004. Тогда L=5000.0,0004=2. Применяя (3), получим

Задача 52. Вероятность попадания в цель при отдельном выстреле равна 0,6. Найти вероятность того, что число попаданий при 600 выстрелах будет заключено в пределах от 330 до 375.

Решение. Формулы Бернулли, Пуассона, асимптотическая формула (2), выражающая суть локальной теоремы Лапласа, позволяют найти вероятность появления события А ровно Т раз при П независимых испытаниях. На практике часто требуется определить вероятность того, что событие А наступит не менее Т1 раз и не более Т2 раз, т. е. число Т Определено неравенствами Т1£Т£Т2. В таких случаях применяют интегральную теорему Лапласа.

Если вероятность наступления события А в каждом из П независимых испытаний постоянна и равна Р (Р отлична от нуля и единицы), а число П достаточно велико, то вероятность того, что событие А в таких испытаниях наступит не менее Т1 раз и не более Т2 раз, вычисляется приближенно по формуле

Имеются таблицы значений функции (см. табл. 2 Приложения). Ф(х) называется функцией Лапласа. Эта функция является нечетной, т. е. Ф(-х)=-Ф(х). Поэтому таблица значений дается только для положительных чисел. Функция Ф(х) является монотонно возрастающей. При неограниченном возрастании Х функция Ф(х) стремиться к 0,5. Если воспользоваться готовыми значениями функции Лапласа, то формулу (4) можно записать так:

По условию П=600, Р=0,6, Т1=330, Т2=375. Находим A И B:

По таблице 2 находим Ф(1,25)=0,3944; Ф(-2,5)=-Ф(2,5)=-0,4938. Подставив эти значения в (5), получим искомую вероятность:

Задача 53. Случайная величина Х распределена по нормальному закону. Математическое ожидание М(Х)=5; дисперсия D(X)=0,64. Найти вероятность того, что в результате испытания Х примет значение в интервале (4,7).

Решение. Если случайная величина Х задана дифференциальной функцией F(X), то вероятность того, что Х примет значение, принадлежащее интервалу (A,B), вычисляется по формуле

Если величина Х распределена по нормальному закону, то

Где А=М(Х) и . По условию S=5, , A=4 и B=7. Подставив эти данные в (6), получим

Задача 54. Считается, что отклонение длины изготавливаемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Стандартная длина (математическое ожидание) A=40 см, среднее квадратическое отклонение S=0,4 см. Найти вероятность того, что отклонение длины от стандартной составит по абсолютной величине не более 0,6 см.

Решение. Если Х – длина детали, то по условию задачи эта величина должна быть в интервале (А-D, а+D), где А=40 и D=0,6. Подставив в формулу (6) A=а-D И B=а+D, получим

Подставляя в (7) имеющиеся данные, получим

Итак, вероятность того, что изготовление детали по длине будут в пределах от 39,4 до 40,6 см, составляет 0,8664.

Читайте также: