Деревья и алгоритмы их обработки
Обновлено: 18.09.2024
Аннотация: В лекции рассматриваются определение и виды деревьев поиска, приемы снижения трудоемкости поиска в древовидных структурах, приводятся описания алгоритмов поиска в двоичных упорядоченных, случайных и сбалансированных в высоту (АВЛ) деревьях, приводятся примеры программной реализации бинарного дерева поиска и АВЛ-дерева.
Цель лекции: изучить алгоритмы поиска на основе деревьев, научиться решать задачи поиска через построение упорядоченного, случайного, оптимального или сбалансированного в высоту деревьев на языке C++.
Поиск данных, являясь одним из приоритетных направлений работы с данными, предполагает использование соответствующих алгоритмов в зависимости от ряда факторов: способ представления данных, упорядоченность множества поиска, объем данных, расположение их во внешней или во внутренней памяти. Поиск – процесс нахождения конкретной информации в ранее созданном множестве данных. Как правило, данные представляют собой структуры, каждая из которых имеет хотя бы один ключ – значение определенного поля конкретной структуры. Ключ поиска – это поле , по значению которого происходит поиск .
Рассмотрим организацию поиска данных, имеющих древовидную структуру. Анализируя дерево только с точки зрения представления данных в виде иерархической структуры, заметим, что выигрыша при организации поиска не получится. Сравнение ключа поиска с эталоном необходимо провести для всех элементов дерева.
Уменьшить число сравнений ключей с эталоном возможно, если выполнить организацию дерева особым образом, то есть расположить его элементы по определенным правилам. При этом в процессе поиска будет просмотрено не все дерево , а отдельное поддерево . Такой подход позволяет классифицировать деревья в зависимости от правил построения. Выделим некоторые популярные виды деревьев, на основе которых рассмотрим организацию поиска.
Двоичные (бинарные) деревья
Двоичные деревья представляют собой иерархическую структуру, в которой каждый узел имеет не более двух потомков. То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). При этом каждое поддерево в свою очередь тоже является деревом. Поиск на таких структурах не дает выигрыша по выполнению по сравнению с линейными структурами того же размера, так как необходимо в худшем случае выполнить обход всего дерева. Поэтому интерес представляют двоичные упорядоченные деревья.
Двоичные упорядоченные деревья
Двоичное дерево упорядоченно, если для любой его вершины x справедливы такие свойства ( рис. 40.1):
- все элементы в левом поддереве меньше элемента, хранимого в x ,
- все элементы в правом поддереве больше элемента, хранимого в x ,
- все элементы дерева различны.
Если в дереве выполняются первые два свойства, но встречаются одинаковые элементы, то такое дерево является частично упорядоченным. В дальнейшем будет идти речь только о двоичных упорядоченных деревьях. Основными операциями, производимыми с упорядоченным деревом, являются:
- поиск вершины;
- добавление вершины;
- удаление вершины ;
- вывод (печать) дерева;
- очистка дерева.
Пример 1. Программная реализация основных операций бинарного дерева поиска.
Алгоритм удаления элемента более трудоемкий, так как надо соблюдать упорядоченность дерева. При удалении может случиться, что удаляемый элемент находится не в листе, то есть вершина имеет ссылки на реально существующие поддеревья . Эти поддеревья терять нельзя, а присоединить два поддерева на одно освободившееся после удаления место невозможно. Поэтому необходимо поместить на освободившееся место либо самый правый элемент из левого поддерева , либо самый левый из правого поддерева . Упорядоченность дерева при этом не нарушится. Удобно придерживаться одной стратегии, например, заменять самый левый элемент из правого поддерева . Нельзя забывать, что при замене вершина , на которую производится замена, может иметь правое поддерево . Это поддерево необходимо поставить вместо перемещаемой вершины.
Временная сложность этих алгоритмов (она одинакова для этих алгоритмов, так как в их основе лежит поиск ) оценим для наилучшего и наихудшего случая. В лучшем случае, то есть случае полного двоичного дерева , получаем сложность Omin(log n) . В худшем случае дерево может выродиться в список . Такое может произойти, например, при добавлении элементов в порядке возрастания. При работе со списком в среднем придется просмотреть половину списка. Это даст сложность Omax(n) .
Случайные деревья
Случайные деревья поиска представляют собой упорядоченные бинарные деревья поиска, при создании которых элементы (их ключи) вставляются в случайном порядке.
При создании таких деревьев используется тот же алгоритм , что и при добавлении вершины в бинарное дерево поиска. Будет ли созданное дерево случайным или нет, зависит от того, в каком порядке поступают элементы для добавления. Примеры различных деревьев, создаваемых при различном порядке поступления элементов, приведены ниже ( рис. 40.2).
При поступлении элементов в случайном порядке получаем дерево с минимальной высотой h (рис. 40.2А), при этом минимизируется время поиска элемента в дереве, которое пропорционально O(log n) . При поступлении элементов в упорядоченном виде (рис. 40.2В) или в порядке с единичными сериями монотонности (рис. 40.2С) происходит построение вырожденных деревьев поиска (оно вырождено в линейный список ), что нисколько не сокращает время поиска, которое составляет O(n) .
Структуры данных и алгоритмы. Теория. Деревья. Основные алгоритмы над деревьями
Дерево – это АТД (абстрактный тип данных) для хранения информационных элементов имеющих нелинейные отношения. За исключением элемента, который находится во главе дерева, каждый элемент имеет родителя, а также ноль или более дочерних элементов. Также говорят что дерево – это множество элементов, среди которых есть один выделенный который называется корнем, а остальные содержатся в N непересекающихся подмножествах, которые называются поддеревьями. Очевидно что дерево относится к классу динамических структур данных наряду с нам уже знакомыми стеком, очередями. С помощью дерева можно представить, например, следующую организационную структуру:

Наиболее известным классическим примером деревьев является генеалогическое дерево.
Также в качестве примера можно привести принятую в большинстве файловых систем организацию с помощью иерархически вложенных директорий и файлов. Наиболее ярко это проявляется в О.С. linux и unix, где файловую систему представляют в виде единого дерева, которое начинается с корневой директории обозначаемой “/”.
Следует помнить, что большинство операций, которые выполняются над деревьями, являются рекурсивными, т.к. деревья имеют рекурсивную структуру – каждое дерево содержит множество поддеревьев.
О деревьях можно судить как об упорядоченных или не упорядоченных. Мы говорим, что дерево упорядочено, если каждому из элементов можно сопоставить порядковый номер: 1,2,3. На рисунках упорядоченные “братья-узлы” представляются слева направо.
Пример упорядоченного дерева: книга. Книга имеет древовидную структуру с делением на разделы, каждый из которых состоит из множества тем, а тема включает отдельные вопросы. Каждый из вопросов также можно разделить на элементарные части – абзацы, картинки, таблицы. Очевидно, что эти элементы имеют четкий порядок следования, нарушение которого приводит к потере смысла книги.
В информатике наиболее часто используются именно двоичные деревья - это деревья, каждый узел которого содержит не более чем два подчиненных ему (дочерних элемента). Бинарное дерево считается правильным, если каждый узел не содержит одного или содержит два дочерних элемента. Таким образом – генеалогическое дерево – это правильно двоичное дерево. В бинарных деревьях дочерние узлы именуют “правый” и “левый”.
С помощью двоичного дерева можно легко представить арифметическое выражение с использованием бинарных операций.
Например, для выражения: (2*3)/(1+1)-(3*7) можно построить следующее дерево:

- 1+3*5-(17*(21-5))
- 2*3*(2-6)*(7-4)*(1-5)
- 8*1*(5/7)*((1+2)/(3-7))

Для каждого узла дерева можно определить понятие глубины. Допустим, V – узел дерева. Глубина узла выражается количество предков V, за исключением самого V. По определению глубина корня равна нулю.
- если узел –корень, то его глубина ноль;
- в противном случае глубина узла V равна 1 + глубина его родителя V`.
Способы представления деревьев: Представление дерева с помощью массива
- P(V) = 2*N - в случае если узел V находится слева от своего родительского узла V*.
- P(V)= 2*N + 1 – а эта формула применима в той ситуации, когда узел V находится правее чем родительский.
Очень важно, что если дерево не полное, то отсутствующим элементам назначаются номера и для них выделяется место в массиве, просто в ячейке с номером “8, 9, 13, 29” и других (согласно приведенному изображению дерева математического выражения) ничего не хранится.

Представление дерева с помощью ссылок
В случае множественного дерева (каждый узел может иметь произвольное количество потомков) возможно, воспользоваться подобным объявлением:
В данном примере DATA_TYPE – тип данных соответствующий хранимому в дереве, например, если у нас дерево математического выражения, то это может быть число или знак арифметической операции. Если дерево служит для хранения генеалогической информации – то в качестве типа каждого узла может быть строка с именем человека, или даже произвольная структура или класс CHuman, описывающий кого-то из предков. Обратите внимание на другое, в структуре присутствует ссылка на узел дерева который является родительским, в общем случае это не требуется, однако при решении многих задач поиска и модификации дерева позволяет их упростить, благодаря подобной ссылке мы можем перемещаться по дереву не только в направлении от корня к нижележащим элементам, но и в обратном порядке.
Под LIST_OF_NODES подразумевается некий контейнер способный хранить внутри себя достаточное количество ссылок на поддеревья. В случае если количество не велико и относительно стабильно, то можно воспользоваться обычным массивом. В случае, когда количество элементом может варьироваться в произвольном диапазоне, то рекомендуется применять один из ранее изученных контейнеров: очередь, дек. Если вы используете средства STL, то можно объявить ссылку на множество поддеревьев так:
Алгоритмы формирования деревьев
До текущего момента все рассмотренные алгоритмы предполагали, что у нас есть построенное двоичное или мульти-дерево. Теперь мы рассмотрим схему формирования деревьев с упором именно на практические направления. Одним из важнейших направлений использования бинарных деревьев является оптимизация задач поиска. Когда мы рассматривали тему поиска, то из двух способов – линейных поиск (затраты порядка O(n)) и двоичного поиска (затраты порядка O(log n)) очевидным было применение именно второго подхода. Однако в этом случае нам было необходимо выполнить сортировку массива данных в противном случае алгоритм не работал. В случае использования двоичных деревьев можно создать такой алгоритм его формирования, что задача поиска в нем нужного элемента также будет составлять порядка O(log n).
Пример: предположим, что нашей программе на вход подается поток чисел (в общем случае не упорядоченный), если мы опишем узел дерева как
И потребуем чтобы все узлы, находящиеся в правом поддереве были больше чем корневой элемент, а все узлы из левого поддерева были не более чем корневой элемент, то в таком случае для последовательности чисел: 6 1 3 7 2 9 4 5 2 будет построено следующее дерево:

Деревья, для которых выполняется вышеописанное соотношение, называются деревьями поиска. В таком дереве, для того чтобы найти нужный элемент на каждом шаге пути необходимо принимать решение о выборе направления в зависимости от того, как соотносятся искомый элемент X и значение текущего узла Vi. Если Vi >= X то в таком случае поиск должен идти именно в левом поддереве, в противном случае в правом. Следует отметить, что получившееся двоичное дерево и соответственно эффективность операций поиска сильно зависит от степени упорядоченности поступающих наборов чисел. В случае если эти значения уже отсортированы, например: 1, 2, 3, 4 то получающееся дерево вырождается и начинает напоминать обычный линейный список.

В идеальном случае дерево должно быть сбалансированным. Напомню, что сбалансированным деревом является то, где количество узлов в правом и левом поддеревьях отличаются не более чем на 1. для повышения скорости работы алгоритма поиска в бинарном дереве также используют прием буфера (барьера). В этом случае все ветви будут заканчиваться не ссылкой на NULL, а ссылкой на этот буферный элемент. То, что у нас получилось можно увидеть на картинке:
Замечания к приведенным алгоритмам
В примере 2 предполагается наличие глобальной переменной GlobalBuffer, которая и является ссылкой на вспомогательный (фиктивный) барьерный элемент. Отметьте, что значение информационной компоненты data для этого буферного элемента перед началом цикла устанавливается в data, что позволяет упростить поиск за счет уменьшения количества операций сравнения. Часто начинающие программисты пытаются реализовать подобный поиск с помощью рекурсии, аргументируя, что раз структура данных рекурсивна то и поиск тоже должен быть таковым. Напоминаю, что настоятельно рекомендуется избегать применения рекурсии везде где это возможно из-за непроизводительных затрат на вызов функции.
Очевидно, что деревья будут вряд ли применяться в задачах, структуры данных которых сформированы и не изменяются на протяжении работы программы. Также очевидно, что на практике деревья должны будут расти и уменьшаться. Рассмотрим пример использования дерева для решения задачи частотного анализа.
Пример: предположим, что есть файл, содержащий некоторый объем текста. Для каждого из слов (как вариант, буквы) содержащегося в файле необходимо выполнить подсчет частоты его встречи. Простейшее решение, которое приходит в голову, это воспользоваться структурой данных типа ХЕШ (ассоциативный массив) в этом случае в качестве ключа будет использоваться само слово, в качестве его значения будет количество повторений. Разумеется, что хеш будет легко эмулировать с помощью двух массивов. В случае если файл содержит достаточно большое количество разных слов, то узким местом данного алгоритма будет поиск позиции, в которой встречается нужное слово. В случае если слова поступают в не отсортированном виде, что вполне ожидаемо, то мы должны будем просматривать в среднем половину от заполненного массива слов пока не найдем искомый. Можно воспользоваться, например, алгоритмом сортировки (здесь наиболее естественно применять метод вставки), мы же рассмотрим применение поискового дерева. Слова в нем будут располагаться в алфавитном порядке, т.е. все слова левого поддерева должны находиться в словаре раньше, чем корневой элемент, соответственно все слова правого поддерева должны находиться в словаре позже, чем корневой элемент (не забывайте, что такое соотношение должно выполняться для всех поддеревьев). Каждый раз, когда на вход программе будет поступать очередное слово будет выполняться поиск его схема идентична той, которая была приведена в таблице выше, если операция поиска была неудачна (функция из примера 1 вернула NULL, а функция из примера 2 вернула ссылку на сам буферный элемент), то необходимо в соответствующую позицию вставить новое слово, и его счетчик количества повторений инициализировать 1. После завершения формирования дерева его можно распечатать. Фрагмент кода решающего данную задачу приводится ниже.
В приведенном выше примере реализованы две версии функции для добавления нового слова в частотный словарь (нового узла в дерево) – одна из них не рекурсивная, вторая рекурсивна. Обратите внимание на то, каким именно образом в не рекурсивной версии обеспечивается модификация ссылки на узел (левой или правой) для родительского узла. В рекурсивной версии от использования двойной ссылки я отказался а, следовательно, был вынужден возвращать из функции ссылку на новое перестроенное дерево и присваивать его родительскому “left” или “right”.
Задание: в приведенном примере отсутствует код по удалению созданного дерева, освобождения занятой памяти. Добавьте его самостоятельно.
Подсказка: в терминах рекурсии операция удаления дерева формулируется практически идентично операции печати элементов. Что означает удалить дерево – сначала следует удалить левое поддерево, потом правое, и, наконец, сам корневой элемент. Когда вы это сделаете, то попробуйте найти также и не рекурсивное решение.
Задание: классической задачей также можно считать построения по заданному входному тексту дерева с перекрестными ссылками. Для каждого слова каждой строки текста необходимо определить информацию о том, в каких именно строках данное слово встречалось, а затем распечатать слова в алфавитном порядке с перечислением номеров строк. Подсказка в данном случае рекомендуется сочетать использование двоичного дерева из предыдущего примера, в каждом, из узлов которого будет храниться ссылка на другой вспомогательный контейнер для хранения номеров строк. Можно воспользоваться списком или деком из ранее рассмотренных тем. В случае если мы будем хранить именно номера строк, то можно пренебречь эффективностью решения задачи и применить фиксированный массив размером не более чем количество всех строк исходного текста. Однако более совершенным будет использование именно списка. Когда вы сделаете это задание, то попробуйте дальше развить пример и добавить необходимость работать с самими строками, а не их номерами, так можно создать глобальный массив с перечислением строк. А каждый элемент списка будет ссылкой на какой-нибудь из элементов массива строк.
Операции над деревьями. Проход дерева.
Методы обхода дерева будем рассматривать на примере двоичного дерева изображенного на следующем изображении (следует отметить, что выбор в качестве пример именно бинарного дерева ни коим образом не ограничивает общности наших рассуждений).

Проход дерева представляет собой систематическое посещение всех его узлов. Наиболее известна схема прямого и обратного прохода.
Прямой проход предполагает, что первое обращение осуществляется к корню дерева, а затем по очереди выполняется рекурсивный проход вдоль каждого из поддеревьев выходящих из корневого элемента. С использованием псевдокода эту операцию можно записать так:
Для приведенного нами выше дерева с буквами последовательность выводимых с помощью прямого прохода букв будет следующей:
Пример: Предположим, задано дерево арифметического выражения. Необходимо сформировать его строковое представление по следующему принципу:
Для дерева описывающего выражение (2*3)/(1+1)-(3*7), строковым представлением будет следующая строка: ( - (/ (* 2 3) (+ 1 1)) (* 3 7)). В данном случае следует применять метод прямого прохода. Обратите внимание на то, что для каждой скобки вначале ее идет знак арифметической операции, а затем операнды, если эти операнды – числа, то они записываются, как есть, если же какой-то операнд представляет собой выражение, то снова рекурсивно применяется правило прямого обхода.
Следовательно с помощью псевдокода алгоритм PrintForm(УзелДереваT) можно записать так:
В данном примере предполагается существование некоторого метода toString() который и печатает значение информационной компоненты каждого из узлов.
Обратный проход
Данный проход в некотором смысле является обратным к алгоритму прямого прохода. Прежде всего, идет посещение всех дочерних узлов и только потом корневого. Для приведенного нами выше дерева с буквами последовательность выводимых с помощью прямого прохода букв будет следующей:
Данный вид прохода применяется в том случае, когда необходимо сначала пройти дочерние элементы, например для подсчета некоторой характеристики и только потом на основании этой характеристики обработка узла.
Пример: рассмотрим задачу печати всех узлов дерева, которые имеют нечетное количество подчиненных узлов. В данном случае рекурсивный алгоритм BackPrintNodes (УзелДерева T) будет выглядеть так:
В приведенном фрагменте кода предполагается, что каждый узел дерева имеет ряд методов для доступа к поддеревьям.
Разумеется, что конкретный код реализации данных методов зависит от того какие именно задачи, какую предметную область представляет данное дерево. Однако обратите внимание на то, что сначала мы выполняем проход по всем поддеревьям накапливая количество всех подузлов которые есть у текущего элемента дерева.
В качестве еще одного пример обратного прохода можно привести определение в каком-либо из файловых менеджеров (far, windows commander, Norton commander) объема занимаемого некоторой директорией. Очевидно, что объем директории состоит из объема дискового пространства для хранения служебной информации непосредственно о директории, также объема занимаемого всеми файлами которые находятся в каталоге, и внимание, объема который занимают подкаталоги. Следовательно, мы снова вынуждены выполнить проход по всем подкаталогам (на всех уровнях вложенности) чтобы определить объем текущего каталога.
Иные способы прохода деревьев
Метод прямого и обратного прохода наиболее часто встречается, однако есть и иные способы, например проход по глубине.
Как вы уже знаете каждый узел дерева имеет глубину (расстояние между ним и корневым элементом). В методе прохода по глубине сначала выполняется проход по все узлам, имеющим глубину X, и только потом выполняется переход к узлам с глубиной X + 1.
Исключение элементов из дерева
- Если узел V не имеет потомков (терминальный узел) то надо просто освободить занимаемую им память, а родительской ссылке на V присвоить значение NULL.
- Если узел V имеет только одного потомка, (например V->left != NULL, а V->right==NULL) в таком случае мы после освобождения ресурсов памяти занимаемых V должны будем родительской ссылке на него присвоить ссылку на потомка V.
- V имеет двух потомков. В этом случае удаляемый элемент следует заменить на либо самый правый
Вспомогательная функция “helperDelete” выполняет спуск вдоль левого поддерева удаляемого элемента все время вправо до тех пор, пока не будет найден элемент, который не имеет правого, обозначим его как “R”, тогда выполняется копирования его значения в узел для удаляемого элемента, а на самом деле удаляется физически (освобождается память) именно элемент R. Если элемент R имеет левое поддерево, то для него выполняется код аналогичный общей схеме удаления для узла, имеющего одного потомка.
Задания по теме деревья
1) Пусть T – бинарное дерево с количеством узлов N. Предположим, что некоторый узел данного дерева V будет называться романским, если количество потомков в его левой ветви отличается от количества потомков правой ветви максимум на 5. Необходимо разработать метод с линейными затратами времени, который найдет все такие узлы дерева V* которые сами не являются романскими, но при этом все его потомки являются таковыми.
2) Необходимо разработать код приложения, который выполняет прямой проход по дереву, не использую методы рекурсии.
3) Длина пути дерева T вычисляется как сумма глубин всех узлов T. Необходимо разработать метод, который с линейными затратами времени найдет длину дерева T.
4) Напишите программу ввода и отображения генеалогического дерева в виде бинарного дерева. При выводе желательно придерживаться следующей схемы отображения, количество отступов перед выводом каждого имени должно быть равно глубине соответствующего узла:
5) Реализуйте бинарное дерево, используя двунаправленную очередь (подсказка: это задание является развитием способа представления дерева в виде массива, но при этом мы не храним пустые (неиспользуемые элементы дерева). Можно использовать в качестве узла дерева структуру из двух полей: информация об узле а также его порядковый номер).
До сих пор мы рассматривали структуры данных, данные в которых располагаются линейно. В связном списке — от первого узла к единственному последнему. В динамическом массиве — в виде непрерывного блока.
В этой части мы рассмотрим совершенно новую структуру данных — дерево. А точнее, двоичное (бинарное) дерево поиска (binary search tree). Бинарное дерево поиска имеет структуру дерева, но элементы в нем расположены по определенным правилам.
Для начала мы рассмотрим обычное дерево.
Деревья

Это дерево показывает структуру компании. Узлы представляют людей или подразделения, линии — связи и отношения. Дерево — это самый эффективный способ представления и хранения такой информации.
Вопросы о деревьях задают даже на собеседовании в Apple.
Двоичное дерево поиска
Двоичное дерево поиска похоже на дерево из примера выше, но строится по определенным правилам:
- У каждого узла не более двух детей.
- Любое значение меньше значения узла становится левым ребенком или ребенком левого ребенка.
- Любое значение больше или равное значению узла становится правым ребенком или ребенком правого ребенка.
Давайте посмотрим на дерево, построенное по этим правилам:
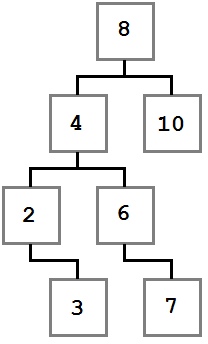
Двоичное дерево поиска
Обратите внимание, как указанные ограничения влияют на структуру дерева. Каждое значение слева от корня (8) меньше восьми, каждое значение справа — больше либо равно корню. Это правило применимо к любому узлу дерева.
Учитывая это, давайте представим, как можно построить такое дерево. Поскольку вначале дерево было пустым, первое добавленное значение — восьмерка — стало его корнем.
Мы не знаем точно, в каком порядке добавлялись остальные значения, но можем представить один из возможных путей. Узлы добавляются методом Add , который принимает добавляемое значение.
Рассмотрим подробнее первые шаги.
В первую очередь добавляется 8. Это значение становится корнем дерева. Затем мы добавляем 4. Поскольку 4 меньше 8, мы кладем ее в левого ребенка, согласно правилу 2. Поскольку у узла с восьмеркой нет детей слева, 4 становится единственным левым ребенком.
После этого мы добавляем 2. 2 меньше 8, поэтому идем налево. Так как слева уже есть значение, сравниваем его со вставляемым. 2 меньше 4, а у четверки нет детей слева, поэтому 2 становится левым ребенком 4.
Затем мы добавляем тройку. Она идет левее 8 и 4. Но так как 3 больше, чем 2, она становится правым ребенком 2, согласно третьему правилу.
Последовательное сравнение вставляемого значения с потенциальным родителем продолжается до тех пор, пока не будет найдено место для вставки, и повторяется для каждого вставляемого значения до тех пор, пока не будет построено все дерево целиком.
Класс BinaryTreeNode
Класс BinaryTree
Класс BinaryTree предоставляет основные методы для манипуляций с данными: вставка элемента ( Add ), удаление ( Remove ), метод Contains для проверки, есть ли такое значение в дереве, несколько методов для обхода дерева различными способами, метод Count и Clear .
Кроме того, в классе есть ссылка на корневой узел дерева и поле с общим количеством узлов.
Метод Add
- Поведение: Добавляет элемент в дерево на корректную позицию.
- Сложность: O(log n) в среднем; O(n) в худшем случае.
Добавление узла не представляет особой сложности. Оно становится еще проще, если решать эту задачу рекурсивно. Есть всего два случая, которые надо учесть:
Если дерево пустое, мы просто создаем новый узел и добавляем его в дерево. Во втором случае мы сравниваем переданное значение со значением в узле, начиная от корня. Если добавляемое значение меньше значения рассматриваемого узла, повторяем ту же процедуру для левого поддерева. В противном случае — для правого.
Метод Remove
- Поведение: Удаляет первый узел с заданным значением.
- Сложность: O(log n) в среднем; O(n) в худшем случае.
Удаление узла из дерева — одна из тех операций, которые кажутся простыми, но на самом деле таят в себе немало подводных камней.
В целом, алгоритм удаления элемента выглядит так:
- Найти узел, который надо удалить.
- Удалить его.
Первый шаг достаточно простой. Мы рассмотрим поиск узла в методе Contains ниже. После того, как мы нашли узел, который необходимо удалить, у нас возможны три случая.
Случай 1: У удаляемого узла нет правого ребенка.
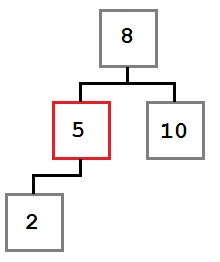
В этом случае мы просто перемещаем левого ребенка (при его наличии) на место удаляемого узла. В результате дерево будет выглядеть так:
Случай 2: У удаляемого узла есть только правый ребенок, у которого, в свою очередь нет левого ребенка.
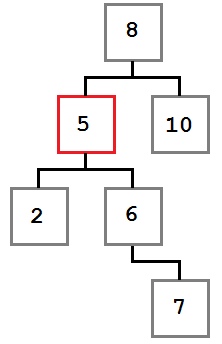
В этом случае нам надо переместить правого ребенка удаляемого узла (6) на его место. После удаления дерево будет выглядеть так:
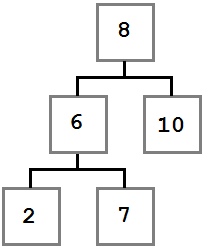
Случай 3: У удаляемого узла есть первый ребенок, у которого есть левый ребенок.
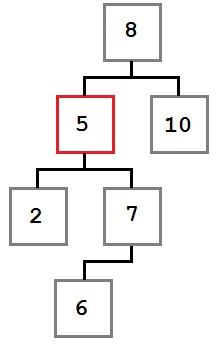
В этом случае место удаляемого узла занимает крайний левый ребенок правого ребенка удаляемого узла.
Давайте посмотрим, почему это так. Мы знаем о поддереве, начинающемся с удаляемого узла следующее:
- Все значения справа от него больше или равны значению самого узла.
- Наименьшее значение правого поддерева — крайнее левое.
Мы дожны поместить на место удаляемого узел со значением, меньшим или равным любому узлу справа от него. Для этого нам необходимо найти наименьшее значение в правом поддереве. Поэтому мы берем крайний левый узел правого поддерева.
После удаления узла дерево будет выглядеть так:
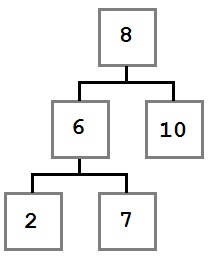
Теперь, когда мы знаем, как удалять узлы, посмотрим на код, который реализует этот алгоритм.
Отметим, что метод FindWithParent (см. метод Contains ) возвращает найденный узел и его родителя, поскольку мы должны заменить левого или правого ребенка родителя удаляемого узла.
Мы, конечно, можем избежать этого, если будем хранить ссылку на родителя в каждом узле, но это увеличит расход памяти и сложность всех алгоритмов, несмотря на то, что ссылка на родительский узел используется только в одном.
Метод Contains
- Поведение: Возвращает true если значение содержится в дереве. В противном случает возвращает false .
- Сложность: O(log n) в среднем; O(n) в худшем случае.
Метод Contains выполняется с помощью метода FindWithParent , который проходит по дереву, выполняя в каждом узле следующие шаги:
- Если текущий узел null , вернуть null .
- Если значение текущего узла равно искомому, вернуть текущий узел.
- Если искомое значение меньше значения текущего узла, установить левого ребенка текущим узлом и перейти к шагу 1.
- В противном случае, установить правого ребенка текущим узлом и перейти к шагу 1.
Поскольку Contains возвращает булево значение, оно определяется сравнением результата выполнения FindWithParent с null . Если FindWithParent вернул непустой узел, Contains возвращает true .
Метод FindWithParent также используется в методе Remove .
Метод Count
- Поведение: Возвращает количество узлов дерева или 0, если дерево пустое.
- Сложность: O(1)
Это поле инкрементируется методом Add и декрементируется методом Remove .
Метод Clear
- Поведение: Удаляет все узлы дерева.
- Сложность: O(1)
Обход деревьев
Обходы дерева — это семейство алгоритмов, которые позволяют обработать каждый узел в определенном порядке. Для всех алгоритмов обхода ниже в качестве примера будет использоваться следующее дерево:
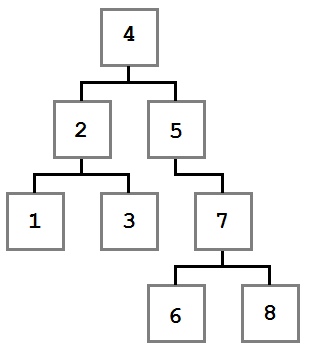
Пример дерева для обхода
Методы обхода в примерах будут принимать параметр Action , который определяет действие, поизводимое над каждым узлом.
Также, кроме описания поведения и алгоритмической сложности метода будет указываться порядок значений, полученный при обходе.
Метод Preorder (или префиксный обход)
- Поведение: Обходит дерево в префиксном порядке, выполняя указанное действие над каждым узлом.
- Сложность: O(n)
- Порядок обхода: 4, 2, 1, 3, 5, 7, 6, 8
При префиксном обходе алгоритм получает значение текущего узла перед тем, как перейти сначала в левое поддерево, а затем в правое. Начиная от корня, сначала мы получим значение 4. Затем таким же образом обходятся левый ребенок и его дети, затем правый ребенок и все его дети.
Префиксный обход обычно применяется для копирования дерева с сохранением его структуры.
Метод Postorder (или постфиксный обход)
- Поведение: Обходит дерево в постфиксном порядке, выполняя указанное действие над каждым узлом.
- Сложность: O(n)
- Порядок обхода: 1, 3, 2, 6, 8, 7, 5, 4
При постфиксном обходе мы посещаем левое поддерево, правое поддерево, а потом, после обхода всех детей, переходим к самому узлу.
Постфиксный обход часто используется для полного удаления дерева, так как в некоторых языках программирования необходимо убирать из памяти все узлы явно, или для удаления поддерева. Поскольку корень в данном случае обрабатывается последним, мы, таким образом, уменьшаем работу, необходимую для удаления узлов.
Метод Inorder (или инфиксный обход)
- Поведение: Обходит дерево в инфиксном порядке, выполняя указанное действие над каждым узлом.
- Сложность: O(n)
- Порядок обхода: 1, 2, 3, 4, 5, 6, 7, 8
Инфиксный обход используется тогда, когда нам надо обойти дерево в порядке, соответствующем значениям узлов. В примере выше в дереве находятся числовые значения, поэтому мы обходим их от самого маленького до самого большого. То есть от левых поддеревьев к правым через корень.
В примере ниже показаны два способа инфиксного обхода. Первый — рекурсивный. Он выполняет указанное действие с каждым узлом. Второй использует стек и возвращает итератор для непосредственного перебора.
Метод GetEnumerator
- Поведение: Возвращает итератор для обхода дерева инфиксным способом.
- Сложность: Получение итератора — O(1). Обход дерева — O(n).
Продолжение следует
На этом мы заканчивает пятую часть руководства по алгоритмам и структурам данных. В следующей статье мы рассмотрим множества (Set).
Третья часть цикла об алгоритмах и структурах данных в JavaScript посвящена древовидным иерархическим структурам.
В предыдущих статьях серии мы имели дело с довольно простыми линейными структурами данных. В них были начало и конец, а все элементы шли друг за другом и имели порядковый номер. Этой простоте приходит конец, когда мы выходим за пределы линии. Сегодня поговорим об очень важной структуре данных – деревьях – и алгоритмах для работы с ней.
Другие статьи цикла:
В самом начале изучения деревья могут сбивать с толку, ведь они используют совсем другой способ упорядочивания данных – иерархический. Но хотя это и может показаться сложным, на практике это обычно оборачивается профитом, так как деревья позволяют применять более эффективные алгоритмы.

Древообразная структура DOM (объектной модели документа).
Структура дерево очень активно используется в разработке, например, всеми любимый DOM – это дерево. В виде дерева можно представить, например, иерархию должностей в компании или каталог библиотеки.
Устройство дерева
В отличие от обычных деревьев, структура данных дерево растет сверху вниз – ее корень находится на самом верху – так удобнее изображать.
- У корневого элемента (на картинке узел со значением 2) есть несколько дочерних узлов (7 и 5), каждый из которых в свою очередь сам является корнем поддерева. Таких уровней может быть сколько угодно.
- Элемент, у которого нет дочерних узлов, называется листом, или терминальным узлом (2, 5, 11, 4). Все остальные узлы (кроме корневого), у которых есть потомки, называются внутренними.
- Каждый узел дерева имеет только одного родителя, не больше. Кроме корневого узла, у которого родителей нет вообще.
- Высота дерева – длина самой длинной ветви (количество ребер). У дерева на картинке она равна 3 – ветка от корня 2 до листа 5. Высоту также можно найти для любого внутреннего узла, например, для узла 6 высота равна 1.
В общем случае число дочерних узлов в дереве не ограничено, но нас в основном интересуют деревья, узлы которых имеют не больше двух потомков (левый и правый). Такие деревья называются двоичными (бинарными) и широко используются во многих задачах программирования. Далее мы будем работать именно с двоичными деревьями.
Кроме двоичных, широкое практическое применение имеют деревья с четырьмя узлами ( дерево квадрантов ). Они используются в геймдеве для организации сетки. Каждый узел в таком дереве представляет одно направление (север-запад, юго-восток и так далее).
Основные операции
Деревья – довольно сложные структуры. Для работы с иерархическими данными они должны предоставлять ряд алгоритмов.
Основные операции, которые нам нужны:
- Добавление нового узла ( add );
- Удаление узла по его значению ( remove );
- Поиск узла по значению ( find );
- Обход всех элементов ( traverse ).
При необходимости этот список можно расширить более сложными алгоритмами:
- Вставка/удаление поддерева;
- Вставка/удаление ветви;
- Вставка элемента в определенную позицию;
- Поиск наименьшего общего предка для двух узлов.
В этой статье мы рассмотрим только основные алгоритмы работы с деревьями, а более продвинутые вы сможете реализовать сами на их основе.
Реализация дерева на JavaScript
Мы реализуем дерево, начиная с корневого узла. Каждый узел будет содержать собственное значение, а также ссылки на дочерние элементы (на левый и на правый) и на родителя. Это очень похоже на связный список, который мы разбирали в прошлой статье.
Высота узла ( height ) вычисляется рекурсивно, на основе высоты его дочерних узлов.
Добавление узлов
Первый алгоритм, который мы должны реализовать для дерева, – это вставка новых узлов. Самая простая реализация не предъявляет никаких правил к расположению элементов, поэтому мы можем просто приписать новый узел к существующему как дочерний (с нужной стороны).
При вставке важно обновить все затронутые ссылки: left или right для родительского узла и parent для дочернего. Если у родителя уже был потомок, его свойство parent нужно обнулить.
Создание дерева
Реализация очень простая, но с ее помощью мы уже можем построить настоящее двоичное дерево, например, такое как на картинке:

Двоичное дерево.
Обход дерева
Теперь нам нужен способ обойти все узлы дерева, чтобы выполнить для каждого из них какую-либо операцию.
Мы разберем два популярных алгоритма обхода дерева:
- поиск в глубину (depth-first search);
- поиск в ширину (breadth-first search).
DFS: Поиск в глубину
Алгоритм начинает с корневого узла и последовательно проверяет все исходящие из него ребра. Если ребро ведет в вершину, которая ранее не рассматривалась, то алгоритм рекурсивно запускается уже для нее, а после его выполнения продолжается проверка других ребер. Таким образом последовательно осматривается каждая ветка дерева.
Визуализация работы алгоритма поиска в глубину.
Запустим перебор для нашего бинарного дерева:
В консоли мы увидим следующее:

Порядок перебора узлов при поиске в глубину
Существует три модификации алгоритма с разным способом перебора узлов:
- обход в прямом порядке , или предупорядоченный обход (pre-order walk). Перебор начинается с родительского узла и идет вниз, к дочерним.
- обход в обратном порядке , или поступорядоченный (post-order walk). Сначала перебираем левого и правого потомков, а потом родителя.
- симметричный обход . Начинаем с левого потомка, потом родитель, потом правый потомок.
Мы реализовали обход в прямом порядке, но можно использовать и другие способы.
BFS: Поиск в ширину
Алгоритм начинает с корневого узла (первый уровень) и двигается по всем ребрам, выходящим из него, перебирая последовательно каждый дочерний элемент (второй уровень). Когда все ребра проверены, алгоритм переходит на следующий уровень и начинает перебирать дочерние элементы дочерних элементов (элементы третьего уровня) и так далее.
Визуализация работы алгоритма поиска в ширину.
Для реализации алгоритма обхода дерева в ширину мы будем использовать структуру данных очередь , которую уже разбирали в предыдущей статье цикла. На каждом шаге извлекаем из нее элемент, который был добавлен первым и перебираем всех его потомков. Каждый потомок также добавляется в очередь.
Можно использовать реализацию очереди из предыдущей статьи или воспользоваться простой очередью на базе JavaScript-массива.
Запустим перебор в ширину:
Результат выглядит так:

Порядок перебора узлов при поиске в ширину.
Бинарное дерево поиска
Одно из самых распространенных использований деревьев – упрощение поиска информации. В первой статье цикла мы говорили о том, что данные проще и быстрее искать в отсортированном массиве. Так вот, их также просто искать в упорядоченном дереве, о котором мы сейчас и поговорим.
Двоичное (бинарное) дерево поиска (binary search tree, BST) – это дерево, в котором элементы размещаются согласно определенному правилу (упорядоченно):
- Каждый узел должен быть "больше" любого элемента в своем левом поддереве.
- Каждый узел должен быть "меньше" любого элемента в своем правом поддереве.
Слова "больше" и "меньше" соответственно означают результат сравнения двух узлов функцией-компаратором.

Пример бинарного дерева поиска.
Благодаря такой сортировке мы можем использовать все преимущества стратегии "разделяй и властвуй" – при поиске элемента можно смело отбрасывать половину дерева. Такие алгоритмы работают гораздо быстрее, чем линейный перебор каждого узла.
Наша реализация предполагает отсутствие в дереве дублей (узлов с одинаковым значением). При необходимости их можно добавить, определив в каком поддереве они должны находиться.
Реализация на JavaScript
Для создания бинарного дерева поиска мы используем уже готовый класс BinaryTreeNode , немного его расширив. Необходимо добавить метод insert , определяющий логику вставки нового узла для сохранения сортировки. Также создадим отдельный класс для самого дерева, который будет хранить ссылку на корневой элемент и делегировать ему рекурсивное выполнение различных методов.
Так как бинарное дерево поиска является упорядоченным, нам еще потребуется функция-компаратор для сравнения элементов.
Метод insert , сравнивает значение нового элемента со значением узла и определяет, в какое поддерево его нужно поместить.
Создадим дерево как на картинке выше:
А теперь обойдем все его элементы, чтобы убедиться, что оно сформировано правильно:

Поиск в бинарном дереве поиска
Все эти сложности со вставкой новых узлов и сортировкой дерева нужны для того, чтобы обеспечить удобный поиск по нему.
Алгоритм поиска в BST очень похож на двоичный поиск в отсортированном массиве, который мы разбирали в первой части цикла. Сравниваем искомое значение с корневым узлом, определяем, в каком поддереве нужно искать, а второе поддерево просто отбрасываем.
Алгоритм поиска рекурсивно проверяет все узлы, пока не найдет подходящий.
Удаление узлов
Удаление узлов из BST – это достаточно сложный алгоритм, так как после удаления узла необходимо восстановить структуру дерева, чтобы оно оставалось отсортированным.
Есть три сценария:
- У удаляемого узла нет потомков (листовой узел).
- У удаляемого узла один потомок (левый или правый).
- У удаляемого узла два потомка.
- Первый случай самый простой и не требует перестройки дерева после удаления.
- Во втором случае после удаления нужно установить связь между родителем удаленного узла и его потомком. Все потомки удаленного узла в любом случае находятся с той же стороны от его родителя, что и сам узел. Поэтому мы записываем их с той же стороны, на которой находился удаленный узел.
- Третий случай самый сложный. Мы должны найти следующий по порядку узел (минимальный узел в правом поддереве удаляемого узла) и поставить его вместо удаляемого.
Для реализации алгоритма удаления нам понадобится несколько вспомогательных методов.
- findMin ищет минимальный элемент в поддереве.
- removeChild удаляет указанный элемент, если он является дочерним для данного узла.
- replaceChild заменяет дочерний элемент на новый.
Теперь добавим в класс BinarySearchTree новый метод remove :
Обратите внимание , в результате удаления возможна ситуация, в которой дерево остается пустым (удаляется корневой элемент, не имеющий потомков). В этом случае мы просто удаляем значение элемента root . Из-за этого требуется небольшая доработка метода insert : если у корневого элемента нет значения, мы просто присваиваем ему новое.
Полный код
Полная реализация бинарного дерева поиска на JavaScript:
Эффективность
Временная сложность всех основных операций в бинарном дереве составляет log(n) – это довольно эффективная структура данных.
| Индексация | Поиск | Вставка | Удаление |
| O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) |
Сбалансированные бинарные деревья
Несмотря на строгие правила сортировки элементов бинарное дерево поиска может оказаться крайне неэффективным.

Вырожденное бинарное дерево поиска.
На картинке изображено валидное бинарное дерево поиска. Для каждого узла соблюдается правило: все узлы в правом поддереве имеют большее значение. Однако такое дерево не позволяет нам пользоваться преимуществами стратегии "разделяй и властвуй", ведь тут нечего отбрасывать. Говорят, что дерево выродилось в список.
Чтобы избежать таких ситуаций, используются более сложные структуры данных – самобалансирующиеся деревья:
Эти деревья используют различные алгоритмы "выравнивания" при вставке и удалении элементов.
Легким движением руки несбалансированное дерево поиска превращается в сбалансированное:

Автоматическая балансировка AVL-дерева.
Визуализация самобалансирующихся деревьев:
Двоичная куча
У кучи также есть корень, а элементы могут иметь дочерние узлы. У двоичной кучи каждый узел может иметь не более двух потомков.
Как и бинарное дерево поиска, куча имеет определенные требования к размещению элементов: все потомки узла должны быть меньше его. Куча, соответствующая этому правилу, называется max-кучей. В ней корень всегда является максимальным элементом.

Пример max-кучи.
Бывают также min-кучи, которые следуют противоположному правилу: все потомки узла должны быть больше его. Таким образом, корнем всегда оказывается минимальный элемент кучи.

Пример min-кучи.
Куча – это самобалансирующаяся структура, при каждой операции она сортирует себя, чтобы все уровни дерева (кроме последнего) были заполнены.
По сути, куча – это очередь с приоритетом. Каждый новый элемент размещается в этой очереди в соответствии с его приоритетом, чем приоритет выше, тем ближе он к началу очереди.
Каждую кучу можно представить в виде линейного массива:

Представление одних и тех же данных в виде дерева и в виде массива.
Чаще всего используется именно линейная реализация, однако дерево более наглядно демонстрирует принцип распределения.
Основные операции
Базовые операции с кучей такие же, как и с очередью:
- найти элемент с максимальным приоритетом (максимальный элемент в max-куче или минимальный элемент в min-куче);
- удалить элемент с максимальным приоритетом;
- добавить в очередь новый элемент.
Реализация
Мы реализуем на JavaScript min-кучу. Для max-кучи нужно только изменить операцию сравнения.
Так как элементы кучи хранятся в виде массива по уровням, нужно определить вспомогательные методы для нахождения потомков и родителей конкретного узла. Мы можем это сделать, так как куча является полным деревом , то есть не имеет пропусков в своей структуре. Индекс нужного элемента в массиве можно вычислить, исходя из его позиции в дереве.
Добавим еще несколько вспомогательных методов для удобных проверок:
Добавление элемента
Сначала новый элемент помещается в самый конец кучи (конец массива), как и в обычной очереди, а затем начинается процесс его поднятия вверх с учетом приоритета. Это рекурсивный алгоритм, который сравнивает элемент с предыдущим и при необходимости меняет их местами.
Получение элемента с максимальным приоритетом
Для получения элемента с начала очереди может быть два метода:
- peek – просмотр без удаления;
- pop – получение элемента и удаление его из очереди.
С peek все понятно, нам просто нужно взять нулевой элемент массива. А вот после удаления необходимо перебалансировать дерево. Для этого мы берем самый последний элемент массива, ставим его в начало и начинаем сдвигать вниз, последовательно сравнивая с его дочерними элементами.
Полный код
Заключение
Деревья – довольно сложная (по сравнению с линейными), но очень интересная структура данных. Об одном из самых популярных ее применений (поиске данных) мы уже поговорили.
Деревья также широко применяются для управления различными иерархиями (каталоги), принятием решений (игры), а также для парсинга и синтаксического разбора выражений. Различные компиляторы основаны именно на деревьях. Значение деревьев в программирование очень велико, так как они позволяют вырваться из линейных структур и обеспечить более удобный в ряде случаев способ представления данных.
В следующей статье мы пойдем еще дальше и поговорим самой нелинейной структуре – графах – и алгоритмах работы с ней.
Читайте также:

