Последовательность чисел фибоначчи описывает размножение кроликов рост веток на деревьях

Обновлено: 18.09.2024

Презентация на тему: " Волшебный мир Фибоначчи. Что такое последовательность Фибоначчи? Существо своей "задачи о размножении кроликов" Фибоначчи сформулировал предельно просто:" — Транскрипт:

1 Волшебный мир Фибоначчи

2 Что такое последовательность Фибоначчи? Существо своей "задачи о размножении кроликов" Фибоначчи сформулировал предельно просто: Существо своей "задачи о размножении кроликов" Фибоначчи сформулировал предельно просто: "Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения?" "Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения?" 1, 1, 2, 3, 5, 8, 13, 21… 1, 1, 2, 3, 5, 8, 13, 21… A(n+1)/A(n)=1,61803… A(n+1)/A(n)=1,61803…

4 История золотого сечения Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хеси-Ра, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления. Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хеси-Ра, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

6 Музыка небесных сфер В 1978 г. русский астроном К. Бутусов рассчитал средние периоды обращения планет Солнечной системы и сопоставил их с "золотой" геометрической прогрессией. Бутусов установил, что отношение периодов обращения соседних планет вокруг Солнца равны либо золотой пропорции 1,618, либо ее квадрату 2,618. Бутусов также устанавливает следующее: В 1978 г. русский астроном К. Бутусов рассчитал средние периоды обращения планет Солнечной системы и сопоставил их с "золотой" геометрической прогрессией. Бутусов установил, что отношение периодов обращения соседних планет вокруг Солнца равны либо золотой пропорции 1,618, либо ее квадрату 2,618. Бутусов также устанавливает следующее: "Частоты обращения планет и разности частот обращений образуют спектр, построенный на основе "золотого сечения"! Иными словами, спектр гравитационных и акустических возмущений, создаваемых планетами, представляет собой консонансный аккорд, наиболее совершенный с акустической точки зрения. "Частоты обращения планет и разности частот обращений образуют спектр, построенный на основе "золотого сечения"! Иными словами, спектр гравитационных и акустических возмущений, создаваемых планетами, представляет собой консонансный аккорд, наиболее совершенный с акустической точки зрения. Мы можем сделать вывод, что утверждения пифагорейцев и Кеплера о "музыке сфер" действительно соответствуют реальным фактам, а не являются только символическими". Мы можем сделать вывод, что утверждения пифагорейцев и Кеплера о "музыке сфер" действительно соответствуют реальным фактам, а не являются только символическими".

7 Задание 1. Группа 1 Группа 1 Привести примеры проявления золотого сечения и числа Фи в природе. Результаты поиска оформить в виде таблицы. Привести примеры проявления золотого сечения и числа Фи в природе. Результаты поиска оформить в виде таблицы. Группа 2 Группа 2 Привести примеры проявления золотого сечения и числа Фи в общественных процессах. Результаты поиска оформить в виде таблицы. Привести примеры проявления золотого сечения и числа Фи в общественных процессах. Результаты поиска оформить в виде таблицы.

8 Выбор темы исследования Проблемный вопрос Состав группы Гипотеза исследования Задачи исследования Существует ли связь отношений среднего периода обращения планет Солнечной системы с уровнями Фибоначчи? Учащиеся 10 класса Пытаемся подтвердить или опровергнуть предположение о том, Пытаемся подтвердить или опровергнуть предположение о том, что отношение периодов обращения соседних планет вокруг Солнца равны либо золотой пропорции 1,618, либо ее квадрату 2,618. Определить наличие взаимосвязи природных явлений с уровнями Фибоначчи.

9 Задание 2. 1) Определить отношение периодов обращения планет Солнечной системы. 2) Проанализировать наличие связи отношений периодов обращения с уровнями Фибоначчи. 3) Определить абсолютную и относительную погрешность отношений относительно уровней Фибоначчи. 4) Результаты вычислений представить в таблице. Задание 2. 1) Определить отношение периодов обращения планет Солнечной системы. 2) Проанализировать наличие связи отношений периодов обращения с уровнями Фибоначчи. 3) Определить абсолютную и относительную погрешность отношений относительно уровней Фибоначчи. 4) Результаты вычислений представить в таблице. Пары планет Отношение периодов обращения Ближайший уровень Фибоначчи Абсолютная погрешность Относительная погрешность

10 Математические основы Теории волн Эллиотта Числа Фибоначчи - математическая основа теории волн. Как признавал сам Эллиотт, математической основой теории стала последовательность чисел, которую открыл Фибоначчи в XIII веке. Числа Фибоначчи - математическая основа теории волн. Как признавал сам Эллиотт, математической основой теории стала последовательность чисел, которую открыл Фибоначчи в XIII веке. Работы Фибоначчи имели огромное значение для последующего развития математики, физики, астрономии и техники. В своей книге "Liber Abaci" Фибоначчи приводит свою последовательность чисел как решение математической задачи - нахождение формулы размножения кроликов. Работы Фибоначчи имели огромное значение для последующего развития математики, физики, астрономии и техники. В своей книге "Liber Abaci" Фибоначчи приводит свою последовательность чисел как решение математической задачи - нахождение формулы размножения кроликов. Числовая последовательность такова: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 (далее до бесконечности). Числовая последовательность такова: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 (далее до бесконечности). Последовательность Фибоначчи имеет весьма любопытные особенности. Последовательность Фибоначчи имеет весьма любопытные особенности. Сумма любых двух соседних чисел равна следующему числу в последовательности. Например: = 8; = 13 и т.д. Сумма любых двух соседних чисел равна следующему числу в последовательности. Например: = 8; = 13 и т.д. Отношение любого числа последовательности к следующему приближается к 0,618 (после первых четырех чисел). Например: 1: 1 = 1; 1: 2 = 0,5; 2: 3 = 0,67; 3: 5 = 0,6; 5: 8 = 0,625; 8: 13 = 0,615; 13: 21 = 0,619 и т.д. Отношение любого числа последовательности к следующему приближается к 0,618 (после первых четырех чисел). Например: 1: 1 = 1; 1: 2 = 0,5; 2: 3 = 0,67; 3: 5 = 0,6; 5: 8 = 0,625; 8: 13 = 0,615; 13: 21 = 0,619 и т.д. Отношение любого числа к предыдущему приблизительно равно 1,618 (величина обратная 0,618). Например: 13: 8 = 1,625. Отношение любого числа к предыдущему приблизительно равно 1,618 (величина обратная 0,618). Например: 13: 8 = 1,625. Отношение любого числа к следующему за ним через одно приближается к 0,382, а к предшествующему через одно - 2,618. Например: 13: 34 = 0,382; 34: 13 = 2,615. Отношение любого числа к следующему за ним через одно приближается к 0,382, а к предшествующему через одно - 2,618. Например: 13: 34 = 0,382; 34: 13 = 2,615.

11 Математические основы Теории волн Эллиотта Для математического изложения своей теории Эллиотт использовал принцип чисел Фибоначчи. Количество волн, образующих тенденцию, совпадает с числами Фибоначчи. Для математического изложения своей теории Эллиотт использовал принцип чисел Фибоначчи. Количество волн, образующих тенденцию, совпадает с числами Фибоначчи. Если внимательно посмотреть на Рисунок, то можно заметить, что полный рыночный цикл состоит из двух больших волн, восьми средних волн, 34 маленьких волн. Аналогично если рассматривать бычий рынок, то можно увидеть, что бычья большая волна состоит из одной большой волны, пяти средних волн, 21 маленькой волны. Если продолжить этот список, то следующим числом бычьих волн будет 89 и т.д. Если внимательно посмотреть на Рисунок, то можно заметить, что полный рыночный цикл состоит из двух больших волн, восьми средних волн, 34 маленьких волн. Аналогично если рассматривать бычий рынок, то можно увидеть, что бычья большая волна состоит из одной большой волны, пяти средних волн, 21 маленькой волны. Если продолжить этот список, то следующим числом бычьих волн будет 89 и т.д. Соответственно, медвежья большая волна состоит из одной большой волны, трех средних волн и 13 маленьких волн. Если же перейти на еще более низкий уровень, то насчитывается уже 55 очень маленьких волн и т.д. Соответственно, медвежья большая волна состоит из одной большой волны, трех средних волн и 13 маленьких волн. Если же перейти на еще более низкий уровень, то насчитывается уже 55 очень маленьких волн и т.д.

12 Задание 3. Группа 1 Группа 1 Исследовать динамику индекса ММВБ за 5 лет. Выписать в таблицу обозначение волн и соотношения волн на графике за этот период. Исследовать динамику индекса ММВБ за 5 лет. Выписать в таблицу обозначение волн и соотношения волн на графике за этот период. Группа 2 Группа 2 Исследовать динамику рынка нефти за 5 лет. Выписать в таблицу обозначение волн и соотношения волн на графике за этот период. Исследовать динамику рынка нефти за 5 лет. Выписать в таблицу обозначение волн и соотношения волн на графике за этот период.

13 Пропорциональный анализ Пропорциональный анализ – это оценка относительных размеров по длительности и амплитуде одной волны по отношению к другой. Амплитуда (измеренная либо в абсолютных, либо в процентных величинах) фактически каждой волны относится к амплитуде смежной, чередующей (через одну*) и/или составной волны как одна из пропорций между числами Фибоначчи. В 1936 Ри в своей книге The Story of the Averages собрал и обобщил сводку по рыночным данным, охватывающей девять бычьих рынков и девять медвежьих рынков на протяжении тридцати шести лет с 1896 по 1932 годы. Бычий рынок развивался дней, в то время как оставшиеся дня были медвежьим рынком. Соотношение между этими цифрами стремится показать, что медвежий рынок длился 61.1% от времени бычьего рынка.

14 Индивидуальность волн Существуют определенные правила пропорций построения волн Эллиотта. Эти правила помогают правильно определить моменты начала построения волн и их длительность. Длины волн измеряются от high до low соответствующей волны. Существуют определенные правила пропорций построения волн Эллиотта. Эти правила помогают правильно определить моменты начала построения волн и их длительность. Длины волн измеряются от high до low соответствующей волны.

15 Пропорциональный анализ Закон природы, управляющий жизнью и развитием, все же допускает огромное разнообразие индивидуальных исходов, и рынок не является исключением. Все, что можно сказать сейчас о пропорциональном анализе, так это то, что сравнение ценовых длин волн зачастую подтверждаются, часто с высокой точностью, применимость пропорций к фондовому рынку найдена в последовательности Фибоначчи. Было весьма впечатляющим, но не удивительным для нас, например, что рост с декабря 1974 по июль 1975 составил как раз 61.8% от предыдущего медвежьего скольжения г.г., или что падения рынка г.г. составило точно 61.8% от предыдущего подъема с декабря 1974 по сентябрь Анализ волновых форм должен преобладать над пропорциональным соотношением волн в последовательности. Применяя пропорциональный анализ, важно понимать и применять волновое исчисление и методы маркировки Эллиотта для того, чтобы определить, от каких точек следует выполнять измерения в первую очередь. Пропорции между длинами, основанные на ортодоксальных уровнях окончания моделей, заслуживают доверие; те, которые основаны на неортодоксальных ценовых экстремумах, нет.

16 Задание 4. Группа 1 Группа 1 Составить прогноз о развитии движения индекса ММВБ на ближайший год и спрогнозировать наиболее вероятные уровни текущих волн. Составить прогноз о развитии движения индекса ММВБ на ближайший год и спрогнозировать наиболее вероятные уровни текущих волн. Группа 2 Группа 2 Составить прогноз о развитии движения цены на нефть на ближайший год и спрогнозировать наиболее вероятные уровни текущих волн. Составить прогноз о развитии движения цены на нефть на ближайший год и спрогнозировать наиболее вероятные уровни текущих волн.

17 Теория циклов Теория циклов существует без малого два с половиной тысячелетия - с тех пор как греческие философы, обобщая накопленные эмпирические знания, попытались проникнуть в суть периодической повторяемости явлений, которая отчетливо проявилась, в природе и была отмечена в развитии общества. И хотя первоначально цикл отождествлялся с кругом, с тождественными повторениями одних и тех же фаз движения, - по мере развития теории циклов на каждой следующей ступени научного познания понятие цикла все более отождествлялось со спиралью, с волнообразными колебаниями, чередованием подъемов и кризисов е годы XX столетия стали "золотым веком" в развитии циклично-генетической теории. Потрясенные глубиной и трагизмом общественных катастроф, крушением научных парадигм и общественных идеалов, наиболее острые умы устремились к глубинным корням и механизмам разразившихся перемен. Усилиями плеяды выдающихся ученых - В.И. Вернадского, А.Л. Чижевского, П.А. Сорокина, Н.Д. Кондратьева, А.А. Богданова, Н.А. Бердяева, Н.И. Вавилова, Ф. Броделя, А. Тойнби, И. Шумпетера и многих других - формировалось новое видение закономерно- неравномерно меняющегося мира. Развитая во второй половине XIX в. теория экономических циклов была дополнена концепцией больших циклов конъюнктуры (циклов Кондратьева), исходными идеями социогенетики (П. Сорокин и Н. Кондратьев), цикличной смены поколений и торжеством генетики в биологии, открытием взаимосвязи солнечных и исторических циклов (А. Чижевский), выявлением цикличных колебаний творческой активности в физике (Т.Д. Райков), формированием моделей цикличной динамики (И. Слуцкий).

18 Главные положения общей теории цикличной динамики Цикличность является всеобщей формой движения в природе и обществе. Траектория цикличного движения характеризуется последовательной сменой фаз; частично совмещаясь, смежные циклы формируют волнообразную динамику процессов. Между последовательно сменяющими друг друга циклами нет перерыва. Циклы никогда не существуют в "чистом" виде; поэтому их так трудно обнаружить и измерить. Взаимодействуют, оказывая резонансное, усиливающее либо, тормозящее влияние, различные циклы. Цикличное время неравномерно. Оно сжимается, частота событий ускоряется в периоды кризисов и революций и замедляется в фазе эволюционного развития, особенно к его концу. Поэтому так трудно строить математические модели цикличного развития, количественно измерять его ритмику.

19 Классическая теория циклов Основой классической теории циклов стало предположение о том, что все вокруг подвержено циклам - рождение, жизнь и смерть, смена времен года, вращение планет и т.д. На финансовых рынках мы также сможем увидеть определенный порядок в периодической смене подъемов и падений.

20 Принципы циклов Для циклов отмечают также четыре основных принципа: суммирования, гармонизации, синхронизации и пропорциональности. Принцип суммирования работает как простое суммирование двух циклических волн. Из них наибольшее влияние на результат суммирования оказывает самый большой цикл. Пример суммирования циклов

21 Принципы циклов Принцип пропорциональности заключается в том, чтобы период и амплитуду короткой волны привести в соответствие с периодом и амплитудой более длинного цикла. Так, если выявленный период длинного цикла равен 40 дням, а короткого - 20, то амплитуда короткой волны должна быть в два раза меньше амплитуды длинной волны (40/20 = 2). Принцип гармонизации обычно используется при сравнении двух циклов. С его помощью более короткий цикл приводят в гармоничное состояние по отношению к более длинному циклу. Принцип синхронизации призван совместить ключевые низы предварительно гармонизированных короткой и длинной волн. Впоследствии можно эти волны просуммировать и получить общий цикл, исходя из выявленных двух. Пример гармонизации и синхронизации циклов

22 Задание 5 Группа 1 Группа 1 Исследовать график американского фондового индекса Dow Jones за последние 100 лет. Определить наиболее вероятное дно рынка в ближайшее десятилетие. Группа 2 Группа 2 Исследовать график американского фондового индекса Dow Jones за последние 100 лет. Определить наиболее вероятные вершины рынка в ближайшее десятилетие.

23 Представление результатов исследований Результаты Электронные таблицы ПрезентацииПубликацииЭссеВикистатьиСайт Аннотированные ссылки Карты знаний С помощью инструментов критического мышления

24 План работы над проектом 1. Лекция "Последовательность Фибоначчи и число Фи". 2. Поиск информации о проявлении числа Фи в природе и обществе. 3. Лекция "Математические основы Теории волн Эллиотта". Отчёты учащихся о результатах поиска информации. 4. Поиск информации о подтверждении Теории волн Эллиотта. 5. Отчёты учащихся о результатах поиска информации. Обработка информации с применением Теории волн Эллиотта. 6. Лекция "Знакомство с пропорциональным анализом". 7. Поиск информации, подтверждающей достоверность применения пропорционального анализа при прогнозировании движения фондового рынка. 8. Отчёты учащихся о результатах поиска информации. Обработка информации с применением пропорционального анализа при прогнозировании движения фондового рынка. 9. Знакомство с Общей теорией циклов. 10. Поиск информации, подтверждающей достоверность Общей теорией циклов. 11. Отчёты учащихся о результатах поиска информации. Обработка информации, подтверждающей достоверность Общей теорией циклов. 12. Подведение итогов на круглом столе, представление собственных результатов исследования.

Последовательность чисел Фибоначчи описывает размножение кроликов, рост веток на деревьях и много чего ещё. Определяется последовательность так: первый и второй члены последовательности равны 1, а каждый последующий — сумме двух предыдущих. Напишите программу, которая выводит первые несколько членов последовательности Фибоначчи — все, не превышающие натурального числа, заданного пользователем.
Формат ввода
Одно натуральное число.

Формат вывода
Числа Фибоначчи, не превышающие введенного числа, записанные по одному в строке.

Вывести сумму заданного числа членов последовательности
Помогите решить, ну никак не получается. Переменные X,Y являются вещественными и вводятся.

Вывести сумму заданного числа членов последовательности
переменные X, Y являются вещественными и вводятся пользователем. Количество слагаемых также.

Найти все нечетные числа последовательности Фибоначи, не превышающие заданного числа
Помогите пожалуйста! Языки Си. Найти все нечетные числа последовательности Фибоначи, не.

Вывести первые n членов треугольной последовательности
Дана монотонная последовательность, в которой каждое натуральное число k встречается ровно k раз.

Задача о размножении кроликов

Одним из наиболее известных математиков эпохи Средневековья по праву считается Леонардо Пизано Фибоначчи. Позже мы расскажем о Фибоначчи и его роли в развитии западноевропейской математики более подробно. По иронии судьбы Фибоначчи, который внес выдающийся вклад в развитие математики, стал известным в современной математике только лишь как автор интересной числовой последовательности, называемой числами Фибоначчи. Эта числовая последовательность была получена Фибоначчи при решении знаменитой "задачи о размножении кроликов". Формулировка и решение этой задачи считается основным вкладом Фибоначчи в развитие комбинаторики. Именно с помощью этой задачи Фибоначчи предвосхитил метод рекуррентных соотношений, который считается одним из мощных методов решения комбинаторных задач. Рекуррентная формула, полученная Фибоначчи при решении этой задачи, считается первой в истории математики рекуррентной формулой.

Существо своей "задачи о размножении кроликов" Фибоначчи сформулировал предельно просто:

"Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения?"

Для решения этой задачи, которая наглядно демонстрируется с помощью рисунка, обозначим через A пару зрелых кроликов, а через B - пару новорожденных кроликов. Тогда процесс "размножения" может быть описан с помощью двух "переходов", которые описывают ежемесячные превращения кроликов в процессе размножения:

Заметим, что переход (1) моделирует ежемесячное превращение каждой зрелой пары кроликов А в две пары, а именно в ту же самую пару зрелых кроликов А и новорожденную пару кроликов В. Переход (2) моделирует процесс "созревания" кроликов, когда новорожденная пара кроликов В через месяц превращается в зрелую пару А. Тогда, если мы начнем в первом месяце со зрелой пары А, тогда процесс размножения кроликов может быть представлен с помощью Таблицы 1.

Дата	Пары кроликов	A	B	A + B
1-го января	A	1	0	1
1-го февраля	AB	1	1	2
1-го марта	ABA	2	1	3
1-го апреля	ABAAB	3	2	5
1-го мая	ABAABABA	5	3	8
1-го июня	ABAABABAABAAB	8	5	13

Заметим, что в столбцах А и В таблицы 1 указаны количества зрелых и новорожденных пар кроликов в каждом месяце года, а в таблице А+В - суммарное количество кроликов.

Изучая последовательности А-, В- и (А+В)-чисел, можно установить следующую закономерность в этих числовых последовательностях: каждый член последовательности равен сумме двух предыдущих. Если теперь обозначить n-й член последовательности, удовлетворяющей этому правилу через F_n, тогда указанное выше общее правило может быть записано в виде следующей математической формулы:

F_n = F_n-1 + F_n-2.

(3)

Такая формула называется рекуррентной формулой.

Заметим, что конкретные значения числовой последовательности, порождаемой рекуррентной формулой (3), зависят от начальных значений последовательности F₁ и F₂. Например, мы имеем F₁ = F₂ = 1 дляA-чисел и для этого случая рекуррентная формула (3) "генерирует" следующую числовую последовательность:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, . .

(4)

Для В-чисел мы имеем: F₁ = 0 и F₂ = 1; тогда соответствующая числовая последовательность для этого случая будет иметь вид:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, . .

Наконец, для (А + В)-последовательности мы имеем: F₁ = 1 и F₂ = 2; тогда соответствующая числовая последовательность для этого случая будет иметь вид:

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . .

В математике под числами Фибоначчи, как правило, понимается числовая последовательность (4). Числа Фибоначчи обладают удивительными математическими свойствами, но об этом - на следующей странице нашего Музея.

О кроликах

Думается, что самое время поговорить о кроликах. Почему именно это животное вошло в историю математики? Как известно, кролик – это млекопитающее отряда грызунов семейства зайцев. Первоначальной родиной дикого кролика в основном считались страны южной части Западной Европы (Испания, Франция, Италия), откуда кролик был привезен человеком во все страны к северу от Альпийских гор. Современная область распространения дикого кролика – вся южная и средняя части Западной Европы, но особенно многочислен он в странах, прилегающих к Средиземному морю, а также в Африке, Азии, Австралии, Новой Зеландии, Америке.

Кроме того, плодовитое кроличье племя, некогда своеобразно повлиявшее на выдающегося математика Италии, в настоящее время взяло в осадное положение итальянский остров Устика (севернее Сицилии). На 1000 жителей этого крохотного островка приходится 100 000 кроликов. В отличие от жителей Австралии коренное население Устики сдается без боя: уже пятая часть жителей эмигрировала с острова.

Вам, конечно же, знакома идея о том, что математика является самой главной из всех наук. Но многие могут с этим не согласиться, т.к. порой кажется, что математика – это лишь задачи, примеры и тому подобная скукотища. Однако математика может запросто показать нам знакомые вещи с совершенно незнакомой стороны. Мало того – она даже может раскрыть тайны мироздания. Как? Давайте обратимся к числам Фибоначчи.

Что такое числа Фибоначчи?

Числа Фибоначчи являются элементами числовой последовательности, где каждое последующее число образуется посредством суммирования двух предыдущих, например: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… Как правило, записывается такая последовательность формулой: F₀ = 0, F₁ = 1, F_n = F_n-1 + F_n-2, n ≥ 2.

Создателем чисел Фибоначчи является один из первых математиков Европы средних веков по имени Леонардо Пизанский, которого, собственно и знают, как Фибоначчи – это прозвище он получил спустя много лет после своей смерти.

О жизненном пути самого Фибоначчи известно крайне мало. Но достоверно известно то, что его задачи пользовались огромнейшей популярностью в математических кругах в последующие века. Одну из таких мы и рассмотрим далее.

Задача Фибоначчи с кроликами

Для выполнения задачи автором были поставлены следующие условия: есть пара новорождённых крольчат (самка и самец), отличающихся интересной особенностью – со второго месяца жизни они производят новую пару кроликов – тоже самку и самца. Кролики находятся в замкнутом пространстве и постоянно размножаются. И ни один кролик не умирает.

Задача: определить количество кроликов через год.

Решение:

Одна пара кроликов в начале первого месяца, которая спаривается в конце месяца
Две пары кроликов во втором месяце (первая пара и потомство)
Три пары кроликов в третьем месяце (первая пара, потомство первой пары с прошлого месяца и новое потомство)
Пять пар кроликов в четвёртом месяце (первая пара, первое и второе потомство первой пары, третье потомство первой пары и первое потомство второй пары)

1 месяц: 1 + 1 = 2

2 месяц: 2 + 1 = 3

3 месяц: 3 + 2 = 5

4 месяц: 5 + 3 = 8

5 месяц: 8 + 5 = 13

6 месяц: 13 + 8 = 21

7 месяц: 21 + 13 = 34

8 месяц: 34 + 21 = 55

9 месяц: 55 + 34 = 89

10 месяц: 89 + 55 = 144

11 месяц: 144 + 89 = 233

12 месяц: 233+ 144 = 377

И эта последовательность может продолжаться бесконечно долго, но учитывая, что задачей является узнать количество кроликов по истечении года, получается 377 пар.

Здесь важно также заметить, что одним из свойств чисел Фибоначчи является то, что если сопоставить две последовательные пары, а затем разделить большую на меньшую, то результат будет двигаться по направлению к золотому сечению, о котором мы также скажем ниже.

Пока же предлагаем вам ещё две задачи по числам Фибоначчи:

Определить квадратное число, о котором известно только, что если отнять от него 5 или прибавить к нему 5, то снова выйдет квадратное число.
Определить число, делящееся на 7, но при условии, что поделив его на 2, 3, 4, 5 или 6 в остатке будет 1.

Такие задачи не только станут отличным способом развития ума, но и занимательным времяпрепровождением. О том, как решаются эти задачи, вы также можете узнать, поискав информацию в Интернете. Мы же не будем заострять на них внимание, а продолжим наш рассказ.

Что же такое рекурсия и золотое сечение?

Рекурсия

Рекурсия является описанием, определением или изображением какого-либо объекта или процесса, в котором есть сам данный объект или процесс. Иначе говоря, объект или процесс можно назвать частью самого себя.

Золотое сечение

Золотое сечение является делением целого на части, соотносящиеся по принципу: большее относится к меньшему аналогично тому, как общая величина относится к большей части.

Приблизительно золотое сечение можно представить в качестве пропорционального деления на две разные части, к примеру, на 38% и 68%. Численное же выражение золотого сечения равно примерно 1,6180339887.

На практике золотое сечение используется в архитектуре, изобразительном искусстве (посмотрите работы Леонардо да Винчи), кино и других направлениях. На протяжении долгого времени, впрочем, как и сейчас, золотое сечение считалось эстетической пропорцией, хотя большинством людей оно воспринимается непропорциональным – вытянутым.

Вы можете попробовать оценить золотое сечение сами, руководствуясь следующими пропорциями:

Длина отрезка a = 0,618
Длина отрезка b= 0,382
Длина отрезка c = 1
Соотношение c и a = 1,618
Соотношение c и b = 2,618

И в заключение ещё немного пищи для ума.

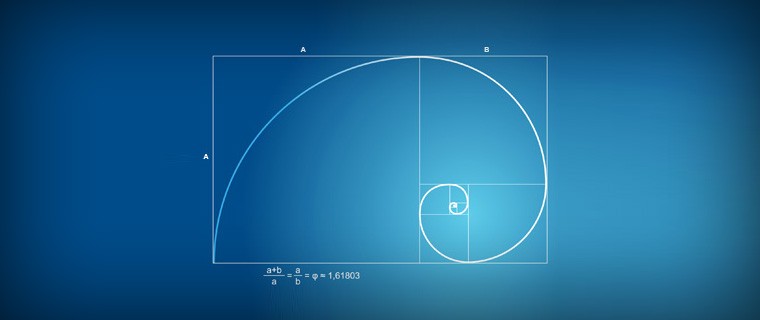
Золотой прямоугольник и спираль Фибоначчи

Вот пример: берём два числа из последовательности Фибоначчи, например 8 и 13, и чертим прямоугольник с шириной 8 см и длинной 13 см. Далее разбиваем основной прямоугольник на мелкие, но их длина и ширина должна соответствовать числам Фибоначчи – длина одной грани большого прямоугольника должна равняться двум длинам грани меньшего.

После этого соединяем плавной линией углы всех имеющихся у нас прямоугольников и получаем частный случай логарифмической спирали – спираль Фибоначчи. Её основными свойствами являются отсутствие границ и изменение форм. Такую спираль можно часто встретить в природе: самыми яркими примерами являются раковины моллюсков, циклоны на изображениях со спутника и даже ряд галактик. Но более интересно то, что этому же правилу подчиняется и ДНК живых организмов, ведь вы помните, что оно имеет спиралевидную форму?

Читайте также: