Выбрать решение по указанному дереву вариантов

Обновлено: 26.07.2024

Специфическим графическим инструментом анализа проблемных ситуаций являются, так называемые, деревья решений. Термин получил свое название от древообразующей структуры схемы.

С помощью этого метода решается целый ряд задач, когда имеются два или более последовательных множества решений, причем, последующие решения основываются на результатах предыдущих состояний среды, т.е. появляется цепочка решений, вытекающих одно из другого. Подобные задачи проще решать с использованием дерева решений, которое представляет собой графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для всевозможных комбинаций.

Для упрощения применения этого метода разобьем его на несколько этапов.

На первом этапе формулируем задачу. Отбрасываем не относящиеся к проблеме факторы, а оставшиеся подразделяем на существенные и несущественные. Далее: определяем возможности сбора информации для экспериментирования и реальных действий; составляем перечень событий, которые с определенной вероятностью могут произойти: устанавливаем временной порядок расположения событий, в исходах которых содержится полезная и доступная информация, и тех последовательных действий, которые можно предпринять.

Рис. 3.1. Составные части дерева решений

Суть третьего этапа состоит в оценке вероятностей состояний среды, т.е. сопоставлении шансов возникновения каждого конкретного события.

Установление выигрышей (или проигрышей, как выигрышей со знаком минус) для каждой возможной комбинации альтернатив (действий) состояний среды составляют четвертый этап.

На пятом этапе решается задача.

Дерево решений состоит из ряда узлов и исходящих из них ветвей. Квадраты обозначают пункты принятия решений (или возможные события), а дуги соответствуют переходам между логически связанными решениями и случайными событиями. Из вершин — решения (квадратов) исходит столько дуг, сколько имеется вариантов (альтернатив), выбор конкретной дуги (вариант решения) осуществляется ЛПР. Из вершины — события также может исходить несколько дуг. Но здесь уже выбор осуществляется случайным образом в соответствии с заданными вероятностями отдельных исходов.

После того, как дерево решения построено, оно анализируется справа налево, т.е. начинать надо с последнего принятого решения. Для каждого решения выбирается альтернатива с наибольшим показателем отдачи (или с наименьшими затратами). Если за принятием решения следует несколько возможных вариантов событий, то выбирается альтернатива с наибольшей предполагаемой прибылью (или с наименьшей предполагаемой величиной затрат).

Рассмотрим задачу максимизации ожидаемой прибыли от акций.

Предположим, что мы владеем акциями стоимостью 1000 у.е. Мы должны принять решение относительно того, держать ли акции, продать их все или купить еще акции на сумму 500 у.е. Вероятность 20%-го роста курсовой стоимости акции составляет 0,6, а вероятность снижения курсовой стоимости на 20% — 0,4. Какое решение необходимо принять с тем, чтобы максимизировать ожидаемую прибыль?

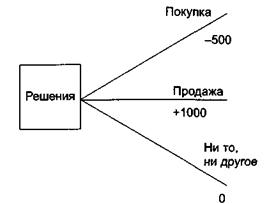
Рис. 3.2. Покупать, продавать или ни то, ни другое

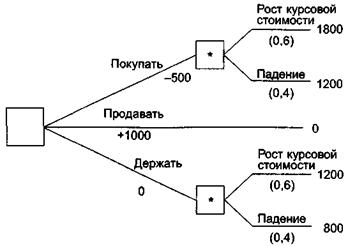
Рис. 3.3. Дерево решений

Начиная с правой стороны и двигаясь влево, производится расчет ожидаемых значений, как это показано на рис. 3.4. Таким образом, ожидаемое значение в блоке вероятностных событий А рассчитывается путем умножения каждой вероятности на значение в конце ветви, т.е. ожидаемое значение в блоке А составляет 0,6 х 1800 + 0,4 х 1200 = 1560 у.е. Аналогично, ожидаемое значение для блока Б составляет 0,6 х 1200 + 0,4 х 800 = 1040 у.е.

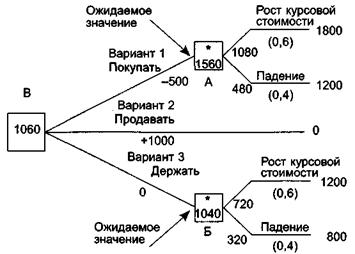Рис. 3.4. Ожидаемые значения

И наконец, можно принимать решение на основании вывода ожидаемых значений по соответствующим ветвям обратно к блоку решений В. Три возможных пути обратно к блоку В дают следующие значения:

Вариант 1: 1560 - 500 = 1060 у.е.

Вариант 2: 0 + 1000 = 1000 у.е.

Вариант 3: 1040 + 0 = 1040 у.е.

Следовательно, на основании данного критерия с целью максимизации ожидаемой стоимости акций мы предпочтем вариант 1. Таким образом, мы решим купить еще акций на сумму в 500 у.е., что даст нам ожидаемую чистую прибыль в 1060 у.е. Это значение показано в блоке В, а путь решения выделен, как показано на рис. 3.4. Следует отметить, что этот простой способ принятия решений, основанный на максимизации ожидаемой отдачи, может не всегда оказаться приемлемым. Например, также необходимо учитывать факторы риска, о чем мы будем говорить в следующем примере.

С помощью дерева решений рассмотрим задачу выбора оптимального проекта реконструкции фабрики — химчистки.

Руководство компании решает реконструировать фабрику — химчистки по одному из трех проектов. Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка (табл. 3.4).

Пример №1 . Требуется принять решение о замене старого оборудования на новое того же вида или его ремонте. Отремонтированное оборудование впоследствии можно частично заменить на новое, более современное, или отремонтировать его заново.
Решение определяется будущим спросом на продукцию, которую производят на этом оборудовании.
Полная замена оборудования экономически оправдана при высоком уровне спроса. С другой стороны, можно отремонтировать старое оборудование и через один год, например, заменить его на новое, более совершенное, или заново его отремонтировать.
В данной задаче процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о замене или ремонте оборудования и решение, принимаемое через один год, относительно частичной его замены и ремонта.
Предполагается, что спрос может оказаться высоким, средним и низким.
Дерево решений имеет два типа вершин: "решающие" и "случайные" (рис.).

Рис. Дерево решений
Начиная с "решающей" вершины 1, необходимо принять решение о полной замене оборудования или его ремонте.
Вершины 2 и 3 являются "случайными". Фирма будет рассматривать возможность установления более совершенного оборудования или повторного ремонта старого в том случае, если спрос по истечении одного года установится на высоком уровне. Поэтому в вершине 4 принимается решение о частичной замене старого оборудования более совершенным или ремонте старого. Вершины 5 и 6 "случайные".
Допускается, что фирма рассматривает эту задачу на пятилетний период. Анализ рыночной ситуации показывает, что вероятности высокого, среднего и низкого уровней спроса составляют соответственно 0,6, 0,3 и 0,1. Замена новым оборудованием того же вида, что и старое, обойдется в 2,5 млн р., а ремонт старого – в 0,8 млн р.
Затраты на частичную замену оборудования более совершенным оцениваются в 1,5 млн р., а повторный ремонт старого – в 0,8 млн р.
Ежегодные доходы для каждой стратегии фирмы следующие.
1. Замена старого оборудования на новое того же вида при высоком, среднем и низком уровнях спроса даёт соответственно 0,95, 0,7 и 0,45 млн р.
2. Ремонт старого оборудования при высоком, среднем и низком уровнях спроса оценивается соответственно в 0,3, 0,15 и 0,1 млн р.
3. Частичная замена оборудования на более совершенное при высоком, среднем и низком уровнях спроса составит соответственно 0,9, 0,6 и 0,4 млн р.
4. Повторный ремонт старого оборудования при высоком, среднем и низком уровнях спроса предполагает 0,3, 0,2 и 0,1 млн р. соответственно.
Определим оптимальную стратегию фирмы в замене оборудования.

Решение.
Оценим результаты каждой стратегии и определим, какие решения следует принимать в "решающих" вершинах 1 и 4.
Вычисления начнем с этапа 2. Для последних 4 лет альтернативы, относящиеся к вершине 4, оцениваются так:
ДЧЗ = (0,9 × 0,6 + 0,6 × 0,3 + 0,4 × 0,1) × 4 – 1,5 = 1,54 млн р.,
ДДР = (0,3 × 0,6 + 0,2 × 0,3 + 0,1 × 0,1) × 4 – 0,8 = 0,2 млн р.,
где ДЧЗ – доход от частичной замены оборудования на более совершенное; ДДР – доход от замены оборудования, прошедшего дважды ремонт.
Так как ДЧЗ > ДДР , то в вершине 4 выгоднее частично заменить оборудование на более совершенное, при этом доход составит 1,54 млн р.
Для дальнейших расчетов в вершине 4 можно оставить одну ветвь, которой соответствует доход в 1,54 млн р. за 4 года.
Вычислим доходы на 1-м этапе для "решающей" вершины 1:
ДЗН = (0,95 × 0,6 + 0,7 × 0,3 + 0,45 × 0,1) × 5 – 2,5 = 1,625 млн р.,
ДЗО = 0,3 × 0,6 × 1 + 0,15 × 0,3 × 5 + 0,1 × 0,1 × 5 +1,54 – 0,8 = 1,195 млн р.,
где ДЗН – доход от замены старого оборудования на новое того же вида; ДЗО— доход от отремонтированного оборудования и дальнейшей замены на более совершенное.
Так как ДЗН > ДЗО , то оптимальным решением в вершине 1 является полная замена старого оборудования на новое того же вида.
Итак, оптимальной стратегией фирмы в замене оборудования является полная замена старого оборудования на новое того же вида, при этом доход составит 1,625 млн р.

среднее предприятие при высоком (низком) спросе – F=1,4 (K=0,38) млн. руб.;
малое предприятие при низком спросе – L=0,25 млн. руб.;
малое предприятие при высоком спросе – М=0,27 млн. руб.;
расширенное предприятие при высоком (низком) спросе дает N=1,6 (P=0,24) млн. руб.;
малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает R=0,2 млн. руб. за остальные восемь лет.

Дерево решений — метод автоматического анализа больших массивов данных. В этой статье рассмотрим общие принципы работы и области применения.

Дерево решений — эффективный инструмент интеллектуального анализа данных и предсказательной аналитики. Он помогает в решении задач по классификации и регрессии.

Правила генерируются за счет обобщения множества отдельных наблюдений (обучающих примеров), описывающих предметную область. Поэтому их называют индуктивными правилами, а сам процесс обучения — индукцией деревьев решений.

В обучающем множестве для примеров должно быть задано целевое значение, так как деревья решений — модели, создаваемые на основе обучения с учителем. По типу переменной выделяют два типа деревьев:

дерево классификации — когда целевая переменная дискретная;

дерево регрессии — когда целевая переменная непрерывная.

Развитие инструмента началось в 1950-х годах. Тогда были предложены основные идеи в области исследований моделирования человеческого поведения с помощью компьютерных систем.

Дальнейшее развитие деревьев решений как самообучающихся моделей для анализа данных связано с Джоном Р. Куинленом (автором алгоритма ID3 и последующих модификаций С4.5 и С5.0) и Лео Брейманом, предложившим алгоритм CART и метод случайного леса.

Структура дерева решений

Рассмотрим понятие более подробно. Дерево решений — метод представления решающих правил в определенной иерархии, включающей в себя элементы двух типов — узлов (node) и листьев (leaf). Узлы включают в себя решающие правила и производят проверку примеров на соответствие выбранного атрибута обучающего множества.

Простой случай: примеры попадают в узел, проходят проверку и разбиваются на два подмножества:

первое — те, которые удовлетворяют установленное правило;

второе — те, которые не удовлетворяют установленное правило.

Далее к каждому подмножеству снова применяется правило, процедура повторяется. Это продолжается, пока не будет достигнуто условие остановки алгоритма. Последний узел, когда не осуществляется проверка и разбиение, становится листом.

Лист определяет решение для каждого попавшего в него примера. Для дерева классификации — это класс, ассоциируемый с узлом, а для дерева регрессии — соответствующий листу модальный интервал целевой переменной. В листе содержится не правило, а подмножество объектов, удовлетворяющих всем правилам ветви, которая заканчивается этим листом.

Пример попадает в лист, если соответствует всем правилам на пути к нему. К каждому листу есть только один путь. Таким образом, пример может попасть только в один лист, что обеспечивает единственность решения.

Терминология

Изучите основные понятия, которые используются в теории деревьев решений, чтобы в дальнейшем было проще усваивать новый материал.

Какие задачи решает дерево решений?

Его применяют для поддержки процессов принятия управленческих решений, используемых в статистистике, анализе данных и машинном обучении. Инструмент помогает решать следующие задачи:

Классификация. Отнесение объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные задачи.

Регрессия (численное предсказание). Предсказание числового значения независимой переменной для заданного входного вектора.

Описание объектов. Набор правил в дереве решений позволяет компактно описывать объекты. Поэтому вместо сложных структур, используемых для описания объектов, можно хранить деревья решений.

Процесс построения дерева решений

Основная задача при построении дерева решений — последовательно и рекурсивно разбить обучающее множество на подмножества с применением решающих правил в узлах. Но как долго надо разбивать? Этот процесс продолжают до того, пока все узлы в конце ветвей не станут листами.

Узел становится листом в двух случаях:

естественным образом — когда он содержит единственный объект или объект только одного класса;

после достижения заданного условия остановки алгоритм — например, минимально допустимое число примеров в узле или максимальная глубина дерева.

n примеров, для каждого из которых задана метка класса Ci(i = 1..k);

m атрибутов Aj(j = 1..m), которые определяют принадлежность объекта к тому или иному классу.

Тогда возможно три случая:

Множество S — пустое множество без примеров. Для него сформируется лист, класс которого выберется из другого множества. Например, самый распространенный из родительского множества класс.

Множество S состоит из обучающих примеров всех классов Ck. В таком случае множество разбивается на подмножества в соответствии с классами. Для этого выбирают один из атрибутов Aj множества S, состоящий из двух и более уникальных значений: a1, a2, …, ap), где p — число уникальных значений признака. Множество S разбивают на p подмножеств (S1, S2, …, Sp), состоящих из примеров с соответствующим значением атрибута. Процесс разбиения продолжается, но уже со следующим атрибутом. Он будет повторяться, пока все примеры в результирующих подмножества не окажутся одного класса.

Третья применяется в большинстве алгоритмов, используемых для построения деревьев решений. Эта методика формирует дерево сверху вниз, то есть от корневого узла к листьям.

Сегодня существует много алгоритмов обучения: ID3, CART, C4.5, C5.0, NewId, ITrule, CHAID, CN2 и другие. Самыми популярными считаются:

ID3 (Iterative Dichotomizer 3). Алгоритм позволяет работать только с дискретной целевой переменной. Деревья решений, построенные на основе ID3, получаются квалифицирующими. Число потомков в узле неограниченно. Алгоритм не работает с пропущенными данными.

CART (Classification and Regression Tree). Алгоритм решает задачи классификации и регрессии, так как позволяет использовать дискретную и непрерывную целевые переменные. CART строит деревья, в каждом узле которых только два потомка.

Основные этапы построения дерева решений

Построение осуществляется в 4 этапа:

Выбрать атрибут для осуществления разбиения в данном узле.

Определить критерий остановки обучения.

Выбрать метод отсечения ветвей.

Оценить точность построенного дерева.

Далее рассмотрим каждый подробнее.

Выбор атрибута разбиения

Разбиение должно осуществляться по определенному правилу, для которого и выбирают атрибут. Причем выбранный атрибут должен разбить множество наблюдений в узле так, чтобы результирующие подмножества содержали примеры с одинаковыми метками класса или были максимально приближены к этому. Иными словами — количество объектов из других классов в каждом из этих множеств должно быть как можно меньше.

Критериев существует много, но наибольшей популярностью пользуются теоретико-информационный и статистический.

Теоретико-информационный критерий

В основе критерия лежит информационная энтропия:

где n — число классов в исходном подмножестве, Ni — число примеров i-го класса, N — общее число примеров в подмножестве.

Энтропия рассматривается как мера неоднородности подмножества по представленным в нем классам. И даже если классы представлены в равных долях, а неопределенность классификации наибольшая, то энтропия тоже максимальная. Логарифм от единицы будет обращать энтропию в ноль, если все примеры узла относятся к одному классу.

Если выбранный атрибут разбиения Aj обеспечивает максимальное снижение энтропии результирующего подмножества относительно родительского, его можно считать наилучшим.

Но на деле об энтропии говорят редко. Специалисты уделяют внимание обратной величине — информации. В таком случае лучшим атрибутом будет тот, который обеспечит максимальный прирост информации результирующего узла относительно исходного:

где Info(S) — информация, связанная с подмножеством S до разбиения, Info(Sa) — информация, связанная с подмножеством, полученным при разбиении атрибута A.

Задача выбора атрибута в такой ситуации заключается в максимизации величины Gain(A), которую называют приростом информации. Поэтому теоретико-информационный подход также известен под название «критерий прироста информации.

Статистический подход

В основе этого метода лежит использования индекса Джини. Он показывает, как часто случайно выбранный пример обучающего множества будет распознан неправильно. Важное условие — целевые значения должны браться из определенного статистического распределения.

Если говорить проще, то индекс Джини показывает расстояние между распределениями целевых значений и предсказаниями модели. Минимальное значение показателя говорит о хорошей работе модели.

Индекс Джини рассчитывается по формуле:

где Q — результирующее множество, n — число классов в нем, pi — вероятность i-го класса (выраженная как относительная частота примеров соответствующего класса).

Значение показателя меняется от 0 до 1. Если индекс равен 0, значит, все примеры результирующего множества относятся к одному классу. Если равен 1, значит, классы представлены в равных пропорциях и равновероятны. Оптимальным считают то разбиение, для которого значение индекса Джини минимально.

Критерий остановки алгоритма

Переобучение в случае дерева решений имеет схожие с нейронными сетями последствия. Оно будет точно распознавать примеры из обучения, но не сможет работать с новыми данными. Еще один минус — структура переобученного дерева сложна и плохо поддается интерпретации.

Для этого используют несколько подходов:

Ранняя остановка. Алгоритм останавливается после достижения заданного значения критерия (например, процентной доли правильно распознанных примеров). Преимущество метода — сокращение временных затрат на обучение. Главный недостаток — ранняя остановка негативно сказывается на точности дерева. Из-за этого многие специалисты советуют отдавать предпочтение отсечению ветей.

Ограничение глубины дерева. Алгоритм останавливается после достижения установленного числа разбиений в ветвях. Этот подход также негативно сказывается на точности дерева.

Задание минимально допустимого числа примеров в узле. Устанавливается ограничение на создание узлов с числом примером меньше заданного (например, 7). В таком случае не будут создаваться тривиальные разбиения и малозначимые правила.

Этими подходами пользуются редко, потому что они не гарантируют лучшего результата. Чаще всего, они работают только в каких-то определенных случаях. Рекомендаций по использованию какого-либо метода нет, поэтому аналитикам приходится набирать практический опыт путем проб и ошибок.

Отсечение ветвей

Поэтому многие специалисты отдают предпочтение альтернативному варианту — построить все возможные деревья, а потом выбрать те, которые при разумной глубине обеспечивают приемлемый уровень ошибки распознавания. Основная задача в такой ситуации — поиск наиболее выгодного баланса между сложностью и точностью дерева.

Но и тут есть проблема: такая задача относится к классу NP-полных задач, а они, как известно, эффективных решений не имеют. Поэтому прибегают к методу отсечения ветвей, который реализуется в 3 шага:

Строительство полного дерева, в котором листья содержат примеры одного класса.

Определение двух показателей: относительную точность модели (отношение числа правильно распознанных примеров к общему числу примеров) и абсолютную ошибку (число неправильно классифицированных примеров).

Удаление листов и узлов, потеря которых минимально скажется на точности модели и увеличении ошибки.

Отсечение ветвей проводят противоположно росту дерева, то есть снизу вверх, путем последовательного преобразования узлов в листья.

Извлечение правил

Иногда упрощения дерева недостаточно, чтобы оно легко воспринималось и интерпретировалось. Тогда специалисты извлекают из дерева решающие правила и составляют из них наборы, описывающие классы.

Для извлечения правил нужно отслеживать все пути от корневого узла к листьям дерева. Каждый путь дает правило с множеством условий, представляющих собой проверку в каждом узле пути.

Если представить сложное дерево решений в виде решающих правил (вместо иерархической структуры узлов), оно будет проще восприниматься и интерпретироваться.

Преимущества и недостатки дерева решений

Преимущества:

Формируют четкие и понятные правила классификации. Например, «если возраст

На этой странице вы найдете решенные типовые задания из контрольных, лабораторных и практических работ по теории игр на тему "Дерево решений" (изучаются в курсах теории рисков, инвестиций, менеджменте, ТПР, МОР, ЭММ и т.п.).

Чаще всего метод дерева решений используют в сложных, но поддающихся классификации задачах принятия решений, когда перед нами есть несколько альтернативных "решений" (проектов, выходов, стратегий), каждое из которых в зависимости от наших действий или действий других лиц (а также глобальных сил, вроде рынка, природы и т.п.) может давать разные последствия (результаты).

Задача состоит в том, чтобы правильно отобразить все возможные варианты развития ситуации (ветви дерева) и конечные результаты, вычислить некоторые показатели (например, ожидаемая прибыльность проекта, затраты и т.п.) и на основе полученных данных принять решение и выборе нужной линии поведения.

Принятие решений с помощью дерева возможных вариантов производится поэтапно:

Построение дерева решений (графа без циклов). Дерево строится по определенным правилам: вершины альтернативных решений, вершины событий, дуги решений, конечные решения - листья вводятся и обозначаются определенным образом в нужном порядке.
Анализ дерева решений : подсчет вероятностей и математических ожиданий (стоимостных оценок решения, EMV), расчет оптимистического и пессимистического прогноза, выбор оптимального решения.

Примеры решений задач: Дерево решений

Задача 1. Вы рассматриваете перспективы создания новой консалтинговой службы. Объем необходимых вложений на начальном этапе $200 тыс. Существует 60%-ная вероятность, что спрос будет высоким в 1-й год. Если спрос будет высоким в первый год, то в последующие годы вероятности высокого и низкого спроса составят 80% и 20% соответственно. Если спрос будет низким в 1-й год, то в последующие годы вероятности высокого и низкого спроса составят 40% и 60% соответственно. При высоком спросе прогнозируемые доходы составят 500 тыс. дол. в год; при низком спросе прогнозируемые доходы равны 300 тыс. дол. в год. Вы можете прекратить предоставлять услуги в любой момент. Затраты, помимо связанных с использованием компьютера, прогнозируются в размере 140 тыс. дол. в год, вне зависимости от уровня спроса.

Если Вы решите не вкладывать деньги в консалтинговую службу, то сможете вложить их на практически безрисковой основе под 20% в год.
Если будет решено организовать консалтинговую службу, Вам необходимо будет решить вопрос с проведением компьютерных расчетов, составляющих основу деятельности. Один возможный вариант - купить сервер.
Срок морального устаревания его 5 лет. Затраты будут состоять из первоначальных расходов в размере 150 тыс. долларов и ежегодных расходов на эксплуатацию в размере 20 тыс.
Альтернативный вариант — арендовать компьютерные ресурсы по мере необходимости. В этом случае затраты на аренду будут пропорциональны спросу и составят 30% доходной части за вычетом оговоренных постоянных расходов в 140 тыс. Во всех случаях никаких других издержек нет.

a. Постройте "древо решений", иллюстрирующее эти варианты и охватывающее 3 года.
b. Стоит организовать консалтинговую службу или безрисковый доход выгоднее? Рассмотрите итоги деятельности за два и три года.
c. Что лучше — купить компьютер или арендовать?
d. Предположим, что после 3 лет деятельности вы сможете продать службу, как отдельный бизнес в среднем за 350 тыс. долларов. Какому ежегодному проценту прироста соответствует полученный вами доход?
e. Четко сформулируйте любые дополнительные допущения, которые вам потребуется сделать.

Задача 2. Фермер может выращивать либо кукурузу, либо соевые бобы. Вероятность того, что цены на будущий урожай этих культур повысятся, останутся на том же уровне или понизятся, равна соответственно 0,25, 0,30 и 0,45. Если цены возрастут, урожай кукурузы даст 30 000 долл. чистого дохода, а урожай соевых бобов — 10 000 долл. Если цены останутся неизменными, фермер лишь покроет расходы. Но если цены станут ниже, урожай кукурузы и соевых бобов приведет к потерям в 35 000 и 5 000 долл. соответственно. Постройте дерево решений. Какую культуру следует выращивать фермеру? Каково ожидаемое значение его прибыли?

Задача 3. Предприятие рассматривает варианты капитальных вложений. Первый вариант предусматривает строительство нового цеха для увеличения объема выпуска продукции стоимостью М1 = 500 млн. руб. При этом варианте возможны большой спрос (годовой доход в размере R1 = 230 млн. руб. в течение 5 последующих лет) с вероятностью p1 = 0,7 и низкий спрос (ежегодные убытки R2 = 90 млн. руб. с вероятностью p2 = 0,3.
Второй вариант предусматривает создание нового предприятия для выпуска новой продукции Стоимостью М1 = 700 млн. руб. При этом варианте возможны большой спрос (годовой доход в размере R1 = 450 млн. руб. в течение 5 последующих лет) с вероятностью p1 = 0,6 и низкий спрос (ежегодные убытки R2 = 150 млн. руб. с вероятностью p2 = 0,4.
При третьем варианте предлагается отложить инвестиции на 1 год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью p1 = 0,8 и p2 = 0,2 соответственно. В случае позитивной информации можно осуществить инвестиции по указанным выше расценкам, в вероятности большого и низкого спроса меняются на p1 = 0,9 и p2 = 0,1 соответственно. Доходы на последующие годы остаются на том же уровне. В случае негативной информации инвестиции осуществляться не будут.
Все расчеты выражены в текущих ценах и не должны дисконтироваться. Нарисовать дерево решений. Определить наиболее эффективную последовательность действий, основываясь на ожидаемых доходах. Какова ожидаемая стоимостная оценка наилучшего решения?

Задача 4. Рассматривается проект покупки доли (пакета акций) в инвестиционном проекте. Пакет стоит 7 млн., и по завершению проект принесет доход 12 млн. с вероятностью 0,6 или ничего с вероятностью 0,4.
При этом через некоторое время будет опубликован прогноз аналитической фирмы относительно успеха этого проекта. Прогноз верен с вероятностью 0,7, то есть, равны 0,7 условные вероятности.
Однако, в случае положительного прогноза пакет порождает до 10,6 млн., а в случае отрицательного подешевеет до 3,4 млн. Требуется составить стратегию действий: покупать ли долю, или ждать прогноза, и совершать ли покупку при том или ином результате прогноза.

Задача 5. Компания "Большая нефть" хочет знать, стоит ли бурить нефтяную скважину на одном из участков, купленных ранее в перспективном месте. Бурение, проведенное на множестве соседних участков, показало, что перспективы не так уж хороши. Вероятность найти нефть на глубине не больше 400 м составляет около 50%. При этом стоимость бурения составит 1.5 млн., а стоимость нефти, за вычетом всех расходов, кроме расходов на бурение, составит 6 млн. Если нефть не найдена на малой глубине, не исключена возможность найти ее при более глубоком бурении. Расходы на бурение, вероятность найти нефть и приведенная стоимость нефти для этих случаев даны в таблице.
a. Постройте дерево решений, показывающее последовательные решения о разработке скважины, которые должна принять компания "Большая нефть". На какую среднюю прибыль компания может рассчитывать?
b. Скважину какой глубины нужно быть готовыми пробурить? (Стоит ли остановиться при достижении определенной глубины, или бурить до предельной глубины?)
c. Какова вероятность найти нефть при бурении (при необходимости) до выбранной вами предельной глубины? Какова полная вероятность найти нефть при готовности бурить до 1500 м?

Дерево решений - это метод, который применяется для принятия решений в условиях неопределенности и риска. Данный метод используется в случае, когда нужно принимать ряд последовательных решений. Дерево решений является графическим методом, который позволяет скоординировать элементы принятия решения, вероятные стратегии (Аi), их последствия (Ei,j) с вероятностными условиями и факторами внешней среды воздействия.

Начинается построение дерева решений с наиболее раннего решения, после разрабатываются возможные результаты и последствия каждого из действий (событий), после вновь определяется выбор направления действия (принимается решение) и так далее до тех пор, пока все последствия результатов решений не будут определены.

Дерево решений составляется на основании 5 последовательных элементов (рисунок 1):

Рисунок 1 – Элементы дерева решений

Простейшее решение

Простейшим решением является выбор из двух вариантов: "нет" или "да". (рисунок 2).

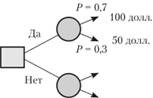
Рисунок 2 - Простейшее дерево решений

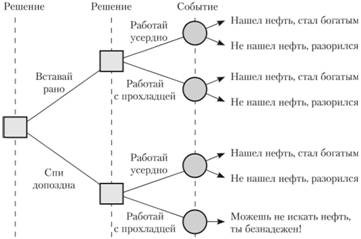
Последовательности решений можно смоделировать следующим образом (рисунок 3):

Рисунок 3 - Дерево (последовательность) принимаемых решений

1) решение: необходимо выбрать между тем, чтобы "Спать допоздна" или "Вставать рано"– простой выбор;

2) решение: необходимо выбрать между тем, чтобы "Работать спустя рукава" или "Работать усердно"– простой выбор;

3) событие: "Найдешь нефть" или нет случается с определенной вероятностью, которая зависит от принимаемых решений.

Поставленные задачи и варианты их решений приведены в таблицах 1 и 2, и отражены на рисунке 4 в виде дерева решений.

Жирным курсивом обозначен путь на дереве, являющийся самым предпочтительным (EV = 820000 долларов) и соответствующий решению, состоящему из элементов "Вставай рано" и "Работай усердно".

Таблица 1 - Вычисление ожидаемых результатов поиска нефти взвешенных по вероятности

Решение: "Вставай рано" + "Работай усердно"	Возможное событие
Решение: "Вставай рано" + "Работай усердно"	Не найти нефть	Найти нефть
Событие: прибыль (убыток), долларов	-200 000	10000 000
Событие: вероятность наступления события	0,90	0,10
Риск = Прибыль (убыток) × Вероятность, долларов	-180 000	1000 000
Ожидаемое значение результата (EV), долларов	1000000-180000 = 820 000

Таблица 2 - Ожидаемые результаты решения "Когда встать и как работать"

Вероятность (найти нефть) = 5% (1- Вероятность) (не найти нефть) = 95%

Ожидаемое значение результатов решения: ( 0 , 05 × 10 000 000 ) + 0 , 95 × ( - 200 000 ) = 310000 долларов

Вероятность (найти нефть) = 10% (1- Вероятность) (не найти нефть) = 90%

Ожидаемое значение результатов решения: ( 0 , 1 × 10 000 000 ) + 0 , 9 × ( - 200 000 ) = 820 000 долларов

Вероятность (найти нефть) = 0% (1- Вероятность) (не найти нефть) = 100%

Ожидаемое значение результатов решения: ( 0 - 10 000 000 ) + 1 × ( - 200 000 ) = - 200 000 долларов

Вероятность (найти нефть) = 1% (1- Вероятность) (не найти нефть) = 99%

Ожидаемое значение результатов решения: ( 0 , 01 × 10 000 000 ) + ( 0 , 99 × ( - 200 000 ) = - 98 000 долларов

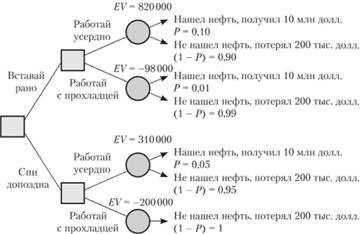
Рисунок 4 - Дерево решений с ожидаемыми значениями результатов(EV), долларов

Дополнительно учтем в примере, приведенном выше, изменение в зависимости от срока окупаемости стоимости проекта.

Установим, что сумма средств, необходимых для поиска нефти, расходуется сразу же. Если находим нефть, то все средства, вложенные в нефтеразведку покрываются сразу же, а доходы от продаж добытой нефти поступают через два года. Чтобы корректно учитывать все данные платежи и поступления, разбросанные во времени, необходимо привести все суммы денежных средств к текущей стоимости.

Установим, что ставка дисконтирования будет принимать значение, равное 20 процентов, тогда таблица 2 будет представлена в следующем виде (таблица 3), а дерево решений (рисунок 4) – в виде, показанном на рисунке 5.

Таблица 3 - Ожидаемая приведенная стоимость и результаты решения "Когда вставать и как работать" с учетом коэффициента дисконтирования

Вероятность (найти нефть) = 5% (1 – Вероятность) (не найти нефть) = 95%

Ожидаемая стоимость: 310000 долл.

Ожидаемая приведенная стоимость: ( 0 , 05 × 10 000 000 ) / 1 , 22 + 0 , 95 × ( - 200000 ) = 157 222 долл.

Вероятность (найти нефть) =10% (1 – Вероятность) (не найти нефть) = 90%

Ожидаемая стоимость: 820 000 долл.

Ожидаемая приведенная стоимость: ( 0 , 1 × 10 000 000 ) / 1 , 22 + 0 , 9 × ( - 200 000 ) = 514 444 долл.

Вероятность (найти нефть) = 0% (1 - Вероятность) (не найти нефть) = 100%

Ожидаемая стоимость: – 200000 долл.

Ожидаемая приведенная стоимость: ( 0 × 10 000 000 ) / 1 , 22 + 1 × ( - 200 000 ) = - 200 000 долл.

Вероятность (найти нефть) =1% (1 - Вероятность) (не найти нефть) = 99%

Ожидаемая стоимость: – 98000 долл.

Ожидаемая приведенная стоимость: ( 0 , 01 × 10 000 000 ) / 1 , 22 + 0 , 99 × ( - 200 000 ) = - 128 555 долл.

Самая эффективная последовательность решений та же (отображен жирной линией путь, который совпадает с решением "Вставай рано" + "Работай усердно", однако изменилось значение ожидаемого выигрыша (514444 долларов), в связи с тем, что учитывалась ставка дисконтирования.

Руководитель организации, выпускающего в настоящее время продукцию X1 в объеме V1тек. = 1000 единиц, считает, что необходимо расширять рынок продукции Х2.

Проведенные маркетинговые исследования определили вилки спроса на продукцию Х2 (V1max = 1000 единиц; V1min = 5000 единиц; V2max = 8000 единиц; V2min = 4000 единиц), а также вероятности низкого и высокого спроса (D1max = 0,7; D1min = 1 -D1max = 0,3; D2max = 0,6; D2min = 1-D2max = 0,4).

Выявлено, что даже минимальный уровень спроса намного превышает имеющиеся мощности организации, которые необходимо использовать для производства обоих видов продукции.

Определен уровень прибыли на единицу продукции каждого из видов (P1 = 1 денежных единиц; Р2 = 0,9 денежных единиц).

Рассчитаны затраты (К = 0,4 * 103 денежных единиц) на удвоение мощности организации (для одновременного производства продукта Х1 в существующем объеме и производства продукции Х2 в эквивалентном объеме) V1тек = 1000 единиц и V2экв = 900 единиц, на увеличение мощности организации под минимальный и максимальный спрос на текущую продукцию (K1min= = 1,4 * 103 денежных единиц и K1max = 2 * 103 денежных единиц) и под минимальный и максимальный уровень спроса на продукцию Х2 (К2 min = 0,8 * 103 денежных единиц и К1max = 1,2 * 103 денежных единиц соответственно).

Необходимо определить рациональность замены продукции и расширения мощностей, под одновременный выпуск продукции в том числе.

Дерево решений и рассчитанные последствия решения отображены на рисунке 5.

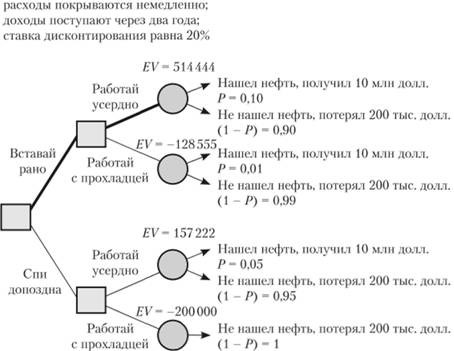
Рисунок 5 - Дерево решений с ожидаемыми значениями приведенных результатов (EV), долларов

Определив результаты решений при производстве продукции одного их видов (Х1 или Х2), выявим эффективные действия во второй точке решений.

Отбросим для этого иррациональные действия по расширению мощностей и данные об ожидаемом выигрыше перенесем в 4 графу. С учетом вероятности существующего спроса на продукты, проведем расчет средней эффективности действий в местах разветвления событий (3 графа). Выявлено, что продолжение производства продукта Х1, при параллельном расширении мощностей является более выгодным вариантом, чем переход на производство продукции Х2 вместо продукции X1.

Однако нами не учитывалась возможность параллельного производства продукции X1 и Х2 при расширении мощностей организации под максимальный уровень спроса. Поэтому проведем еще одно ответвление из первой точки принятия решения, соответствующее этому варианту решения. Эффективность этого варианта состоит из эффективности первого варианта и второго варианта (Э1 и Э2) за минусом вложений на первоначальное удвоение мощностей организации. Эффективность этого варианта самая высокая, поэтому варианты 1 и 2 необходимо вычеркнуть.

Вывод. Необходимо существенно развивать мощности и одновременно выпускать два вида продукции.

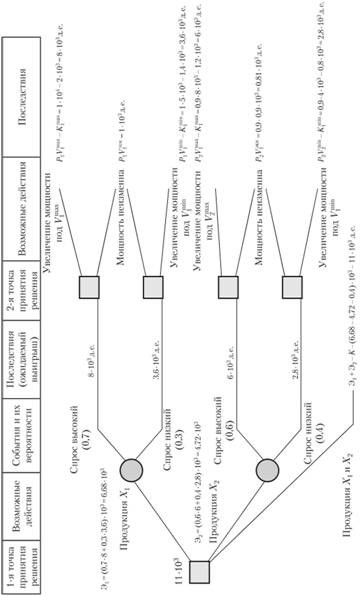
Рисунок 6 - Дерево принятия решений при определении стратегии организации

Представленная схема решения немного упрощена, так как мы не рассматривали варианты привлечения резервов по выпуску продукта одного вида при минимальном уровне спроса для производства продукции другого вида, лимиты по вложениям денежных средств (в условиях задачи для этого недостаточно данных).

Читайте также: